
 |
... |
FALSIFICATION of COMPUTATIONAL MODELS
|
... |
The assumption that the Action Potential of Hodgkin and Huxley is a continuous function of time based on a linear mechanism are refutable and must be discarded, based on the available laboratory data and more recent information. Computational models based on their set of simultaneous differential equations, involving a fourth power term to describe the variation in sodium and potassium impedances of the axolemma must also be discarded.
The initial goal of this page was to provide a rigorous review of the null hypothesis and working hypothesis presented by Hodgkin &l Huxley in a series of papers beginning in 1938 and culminating in a coordianted series of at least four papers in 1952. However, this degree of rigor is impossible based on the fact they did not state a formal null hypothesis that they intended to prove, modified their informal null hypothesis as they proceeded through the presentation, and did not provide a credible working hypothesis as a result of their work.
Hodgkin & Huxley struggled mightily with the problems associated with;
They note (page 506) "there is little hope of calcuating the time course of the sodium and potassium conductaces from first principles." They continue, "our object here is to find equations which describe the conductances with reasonable accuracy and are sufficiently simple for theoretical calculation of the action potential and refractory period." Later investigators have routinely remarked counter to their position;
Attempts by Frankenhauser & Huxley, and by Clay et al. have failed to confirm the utility of the set of equations proposed by Hodgkin & Huxley in paper 1952d. Numerous other attempts to use them have resulted in even more complex equivalent circuits with additional current paths in parallel.
No confirmation of their proposed "special charged molecule" (page 503) has ever appeared in the literature. Its presence is critical to their explanation of the fourth power or higher exponent in the expressions for the sodium and potassium conductances.
- - - -
It is not appropriate for this investigator to put words in the mouths of Hodgkin & Huxley to describe their null or working hypotheses; but it is the only way to refute their hypotheses.
The original partial differential equations proposed by Hodgkin and Huxley (H&H) are themselves based on two null hypotheses that are refuatable and must be discarded.
First, that the chordate Action Potential is also present in the giant axon of the squid Loligo. This null hypothesis was questionable based on the work reported by Hodgkin himself in 1949. It was also found not reproducable by Clay, who tried to reproduce their results for over 25 years during 1985-2010.
Second, that the chordate Action Potential waveform is a continuous function of time. This hypothesis is refuted by more precise data recordings from many laboratories and must be discarded.
The symbology used to describe their proposed circuit diagram for a stand-alone axolemma is totally inappropriate. The symbol they use for a general impedance is only appropriate for a resistive element independent of both voltage and time. Their general impedance associated with both sodium and pottasium are functions of both the applied voltage and of time. An alternate symbol must be used. Note also that their equations for gna and gk both incorporate an exponential time function. Such a function implies this equation describes a complex circuit configuration which includes a reactive element. Such a complex circuit configuration cannot be represented by the symbol for any resistor, fixed or variable. Raising an expression including an exponential term to a power suggests the equivalent circuit might consist of a multiple-section electronic filter.
This page will present the evidence that refutes the Hodgkin & Huxley (H&H) neuron of Action Potential generation. and offer an alternate analysis of the Action Potential waveform.
- - - -
A mathematical model of Action Potential generation was proposed in the 1949- 1952 time period that was based totally on empirical exploration without an adequate null hypothesis preceding the laboratory investigation. It was based on;
As a result, the mechanism of Action Potential generation and the mathematical framework suggested by Hodgkin and Huxley occurrred in mid 20th Century;
This page will summarize the problems with the Hodgkin and Huxley Neuron and the reasons it is refuted by the greater knowledge base at the start of the 21st Century and the data from laboratory investigations of the last half of the 20th Century. Support for this page will be found in Chapter 9 of the text, "The Neuron and Neural Systems; A 21st Century Paradigm" available on this website.
Two areas require review before proceeding; the state of the Scientific Method as employed in biological research and the definitions of several critical terms during the mid-20th Century and the beginning of the 21st Century.
Restating the phylosophical underpinning of the Scientific Method espoused by Popper;
Action Potential-
Orthodromic stimulation- The stimulation of a neuron by means compatible with its normal in-vivo operation; stimulation not involving changing the parameters of a circuit or introducing an alternate current path.
Parametric stimulation- The stimulation of any circuit by a means different from its normal mechanism of stimulation. Typically involving the introduction of a current into the axoplasm of a neuron by a path not associated with the Activa within that neuron or the electrostenolytic circuit normally charging that axoplasm.
Impulse stimulation- Stimulation involving a voltage or current pulse of short duration relative to the shortest time constant of any portion of the circuit under evaluation. Generally used to record the transient response to that impulse and thereby determine the values of the circuit elements of the network. This determination requires removal of all active elements from the network before application of the impulse.
Pulse stimulation-Stimulation involving a voltage or current pulse of longer duration than at least one of the time constants of the portion of the circuit under evaluation. Generally used to emulate the normal stimulation of the circuit under evaluation.
- - - -
To a remarkable degree, Hodgkin and Huxley carried out a program of empirical research without incorporating any explicit null hypothesis relating to their program. As was (and is) common, they relied heavily upon the loosely documented consensus of their peers to define the scientific facts of the time (Ex. page 389 of Hodgkin, 1951). Unfortunately, their work became immortalized to a significant degree without significant activity designed to repeat it until the time of Clay (reporting over a 25 year period (1985-2010 without achieving significant corraboration).
Hodgkin was a well trained physiologist and mathematician of his day. These fields were limited in that day compared to the present (Ex. he was unable to obtain a closed form solution, either the general or particular solution, to his empirically derived partial differential equations of 1952). Hodgkin did not seem to appreciate the difference between the symbolic form of differential equations when stated in their differential form absent the necessary boundary conditions, and their ultimate complete solution based on those boundary conditions.
Hodgkin's interests were broad and his approach cautious (Ex. "Great caution must be exercised in applying conclusions about invertebrate nerve to the excitable cells of vertebrates," Hodgkin,1948, page 165.
Hodgkin was aware of the controversy over whether the presence of sodium ions in the extraneural matrix was required for neuron operation (Ex. Hodgkin, 1951, page 370)
Hodgkin & Huxley were not as well versed in electronics, and they were largely unaware of the results of military research during the Second World War which was only then being documented outside their discipline (Ex; the Radiation Laboratory Series of books published in Cambridge, Massachusetts and New York from 1948 to 1953). The relaxation oscillator suggested by this author as a critical mechanism within the neural system was first widely documented as a result of this war-work (Glasoe & Lebacqz). The transistorized version first appeared after the H & H work (Ex. Gray, 1954, pp 819-825).
Finally, in their last 1952 paper (page 541 of paper 1952D), they were careful to note, "The range of phenomena to which our equations are relevant is limited in two respects: in the first place, they cover only the short-term responses of the membrane, and in the second, they apply in their present form only to the isolated squid giant axon."
They were unable to prevent the community from associating their studies with a much wider range of complete neurons (rather than just the axon of a debrided squid locomotion neuron).
Unfortunately, the fame that came to Hodgkin & Huxley based on their 1952 papers clouded, and effectively inhibited, the field of neuron research for a considerable period. In 1985, Clay began an extended program to repeat the work of Hodgkin & Huxley with limited success (even though he dedicated over 25 years to the task. Beginning with the general introduction of the digital computer, it became popular to "solve" the partial differential equations of the 1952 papaers using numerical methods. This approach did not require any validation of the appropriateness of the individual partial differential equations.
Hodgkin was exploring the neural signals related to crustaceans of the common littoral crab Carcinus maenas in 1951. He noted at the time, When joined by Huxley, their investigations centered on Mollusca, primarily because it was known that the squid (among them Loligo) exhibited a "giant axon" associated with one of its neurons. This large size offered conveniences related to laboratory protocols. They did not offer any discussion of the similarity of the nervous systems of these distinctly different members of the phylogenic tree and members of Chordata.
The term Action Potential was poorly defined in their time, and they offered no precise definition to accompany their needed, but absent, null hypothesis. Figure 2 from Hodgkin, 1951 shows the range of waveforms they considered to be action potentials. The curvatures in the tracings illustrate the primitive capabilities of oscilloscopes of the time (note the higher quality, at a slower time base, of the string galvonometer recording in frame E).
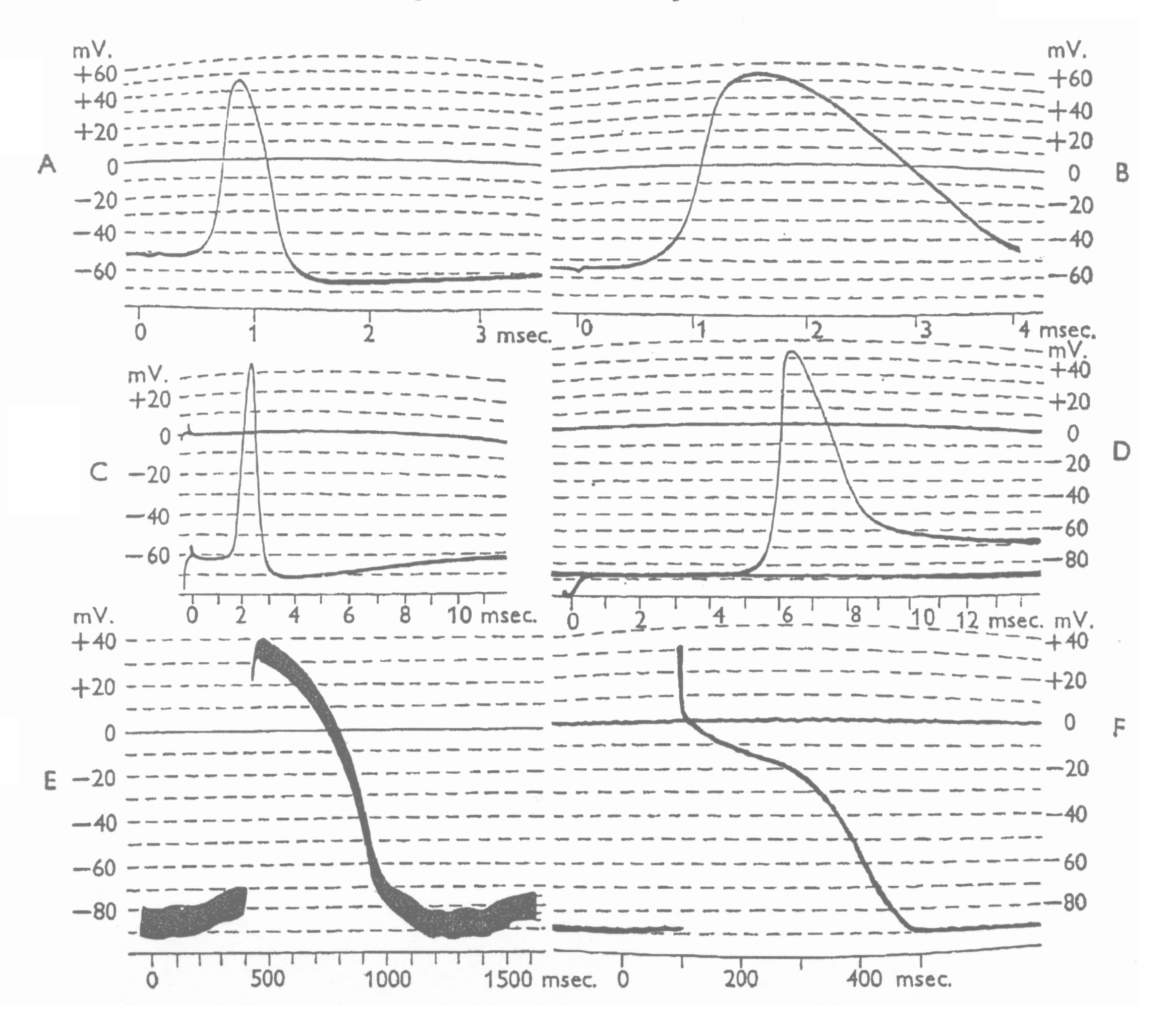
It is noteworthy that none of these waveforms exhibit any threshold potential such as normally associated with an action potential used in signaling. Neither does any of the waveforms exhibit any amplified copy of the stimulating waveform in the voltage range below threshold. The waveform in D is labeled the response from a neuro-affector (a frog muscle fibre) and is not a nominal action potential. Based on this work, E and F are not typical action potentials but are neuro-affector waveforms associated with the mini-neural system of the heart derived from cardiocyte cells (note their extended duration which is not compatible with a signaling function). The characteristics of the waveforms in E & F are developed in detail in Chapter 20 on the mini-neural systems of chordates in "The Neuron and Neural System: A 21st Century Paradigm."
Note the strong suggestion of a switching operation in frames D & E after the sharp rise in the leading edge of the pulse. This type of waveform is very difficult to describe mathematically under the continuity assumption without employing an infinite series of harmonic components.
- - - - -
The description of their protocol makes it quite clear they made little effort to preserve the functionality of the complete giant neuron of their squid. They mutilated the neuron to a significant degree in-vitro by;
As a result of these actions, it is difficult to harmonize their putative theory of neural operation with the current scientific record. The goal of this page is to highlight these conflicts and to show the Hodgkin and Huxley neuron does not provide a mathematical foundation for the development of computational models of a real neuron generating Action Potentials.
Hodgkin & Huxley attempted to manipulate a wide range of empirical data collected by the community during the first half of the 20th Century. The results of their analysis contain many uses of "if" and "must". They attempted to rationalize their after-the-expeirment-hypothesis using a very simple multiple parallel branch electrical network limited to only capacitors,batteries and variable resistors.
Upon seeing this network, any trained electrical engineer (or electronics hobbyist) recognizes it can be replaced by a single capacitor, a single battery and a single variable resistance. To counter this obvious simplification of their network, they were forced to introduce an "Independence Principle" and other semantic crutches, such as the arbitrary and binary functions of time labeled in the m, n, o, p series. These arbitrary multiplier coefficients had the effect of recognizing different mechanisms were occuring during the rising and falling portions of their waveforms.
Their Independence Principle was never demonstrated or reasserted in later writings. More recent attempts to explain the operation of the squid axon under conditions similar to thosee of Hodgkin & Huxley have employed as many as 12 parallel branches. A recent variant by xxx even uses a new symbol for a resistor that may imply it is combined with a perfect diode, or some other undefined isolation mechanism.
Attempting to recover a null hypothesis as perceived by two or three people sixty years ago is difficult at best. They worked in a time of much simpler technologies. Knowledge of electro-chemstry was limited, knowledge of elctrolytic chemistry was extremely limited, and electrostenolytic chemistry was totally unknown. There were major limitations on our understanding of bases and acids (Lewis versus Bronsted concepts) in chemistry, sigma and pie bonding among organics was poorly understood, and coordinate chemistry was completely unknown. Similarly, liquid crystalline chemistry and its semiconducting characteristics were totally unknown. The concepts of electrons and holes moving within the energy band structures of liquid crystals was totally unknown. In fact, the discovery of the man-made transistor had just been announced. Even the simplest semiconducting properties of the transistor were under intensive investigation.
The internal structure of biological lemma was totally unknown and conceptual caricatures were the order of the day. The fact that a lemma consisted of back-to-back amphophilic phospho-lipids was totally unknown.
The impedance level of available instrumentation was typically limited to below a few megohms under the best conditions, and far below the nominal 10-100 megohm regime of the neurons.
They did not anticipate the myelinated neuron was found predominantly, if not exclusively, among the chordates. They did not anticipate a different role or operating characteristic for myelinated neurons. They did not anticipate the giant neuron of the squid might have a unique purpose.
Because of the above technological limitations, Hodgkin & Huxley were hard pressed to enunciate a null hypothesis beyuond the trivial, as viewed by the modern researcher. They were necessarily limited to an exploratory research program based on limited knowledge of where the program might lead. As a result of their program, they developed simple conceptual models and enunciated principles, like their independence principle, that were never confirmed by others.
It is clear that their null hypothesis would have been a short one;
Based on their experiments, their limited knowledge base and their limited mathematical base, the empiricists Hodgkin & Huxley developed a working hypothesis of the neuron (Part I of 1952D) that could be tested by future empiricists.
They differentiated between a "membrane" and propagating action potentials (page 519)
Following the presentation explaining their experiments, H & H summarized their work in the paper labeled 1952D. The complexity of this summary leads to considerable obfuscation. However, it is important to note their first major conclusion, (page 506) "there is little hope of calcuating the time course of the sodium and potassium conductances from first principles." They continue, "Our object here is to find equations which describe the conductances with reasonable accuracy and are sufficiently simple for theoretical calculation of the action potential and refractory period." The omission of the word theoretical appears justified, since they did not offer a theory based result. They go on, "For the sake of illustration we shall try to provide a physical basis for the equations, but must emphasize that the interpretation given is unlikely to provide a correct picture of the membrane." The term theoretical could be used as an alternate for correct in this last statement.
The above quotations show that H & H did not offer a working hypothesis of neuron operation based on their experimental investigation. They only offered a set of equations curve-fit to data points attributed to the movement of sodium and potassium ions through their putative "active" axolemma membrane. Their stated goal was to provide a set of equations that could be used to calculate nominal action potentials.
After making the above statements, Hodgkin & Huxley proceeded to make a number of statements showed a naivite (possibly due to a lack of education in the solving of differential equations).
First, they suggested the solution of a third degree differential equation raised to the first power was the same as the solution of a first order differential equation raised to the third power. While the cubic equation has three distinct roots, two of which are typically complex, the first order equation has only one root, and the cube of that first order equation typically has three equal real roots. While the solution of the cubic can diverge from the baseline at a minimal slope at time zero, the solution to the first order equation, and all higher powers of this equation diverge from the baseline abruptly at time zero. Their statement on page 509 that raising the power of the first order equation from three or four to five or six might introduce a greater amount of delay in the solution departing the baseline at time zero appears to be naive.
Second, they assert the solutions to the second order differential equation with one independent variable (Eq 27 on page 522) is the same as the solutions to a second order equation in two independent variables (the equation between Eq 29 and 30 on page 522). The solution to their second order equation in two independent variables (the General Wave Equation of Maxwell) is quite unique and was very well known at that time. Furhtermore, their coefficient theta (Q) is not an arbitrary coefficient. It is the velocity of the traveling wave in Maxwell's Equation and is given by a term incorporating the fixed parameters in the General Wave Equation. Contrary to their statement, the velocity of the traveling wave is known in advance based on the parameters in the equation.
Unaddressed in the H & H discussion is the fact that Q takes on a different mathematical character depending on the character of the transmission line. For a lossy RC cable, Q is a complex number. Such a mathematical condition is not acceptable physiologically. Alternately, a loss-free LC cable exhibits a Q that is real. Such a cable exhibits a real group velocity and real phase velocity.
Third, they explored the static current-voltage characteristics of their membrane in the 1952a paper. On page 464, they described two functions they define as "chord conductances" (a term foreign to current electronics) for the putative transport of sodium and potassium ions through the axolemma. It is important to note the two functions overlay each other (with at most a 10 mV offset). These functions are more directly described by the diode equation as described below. They are in fact the diode characteristic of the pedicles along their axolemma left after debriding the axolemma of the associated dendrites of subsequent neurons. The figures are entirely independent of the presence of sodium or potassium ions within or outside of the membrane.
In their 1952 series of papers, H & H did review their conclusions (page 500) before developing the above equations. They totally reversed an axiom of their earlier null hypothesis of 1949 as noted on page 502, they no longer supported the position that, "sodium ions do not cross the membrane in ionic form but in combitation with a lipoid soluble carrier which bears a large negative charge and which can combine with one sodium ion but no more."
Based on their experimental findings, the null hypothesis developed above requires significant modification to arrive at a surviving "working hypothesis."
Prior to page 503 of the 1952d paper, the working hypothesis of Hodgkin & Huxley retained major parts of the null hypothesis and is expanded to;
The material in the last paper in their 1952 series (1952d) did not converge to a working hypothesis without the introduction of an additional concept. The introduction of the concept of pores or gates in their previously homogeneous axolemma, with a new mechanism based on their interpretation of the the Boltzmann Principle, led to a significantly different working hypothesis. It no longer involved the flow of alkali and alkali-earth ions through a homeogeneous biological lemma. It involved the flow of such particles through discrete pores or gates in such a lemma. The working hypothesis became;
A series of key experiments provide more than adequate falsification of the chemical theory of the neuron.
It is difficult to define any null hypothesis related to the Hodgkin & Huxley neuron since they did not offer such a hypothesis, except after the experiments were completed.
The current experimental database and theoretical framework of the neural system based on its electrolytic characteristics clearly conflict with the Hodgkin & Huxley neuron of 1952. Therefore, their model dating from the mid 20th Century is refuted.
With the refutation of the Hodgkin & Huxley conceptual model of the neuron, subsequent computational models based on that conceptual model, and set of initial partial differential equations, are also refuted.
A replacement and testable (falsifiable) null hypothesis is presented below based on the neuron containing an active semiconductor element unknown to Hodgkin and Huxley. It is offered as testable (falsifiable) at the current time using current technology.
It is important to note, the investigators whose work in discussed below, failed to explore the fundamental framework of the H & H hypothesis; were these investigators talking about all neurons, were they comfortable that all neurons were alike (even across phylogenic lines), did they support the position that the dendrites of a neuron were not functional, etc.?
The following figure shows the waveforms purported to be Action Potentials by Hodgkin, Huxley & Katz (1952, page 433) at 23 Celsius, and a more recent recording of Action Potentials by Schwartz & Eikhof, 1987.
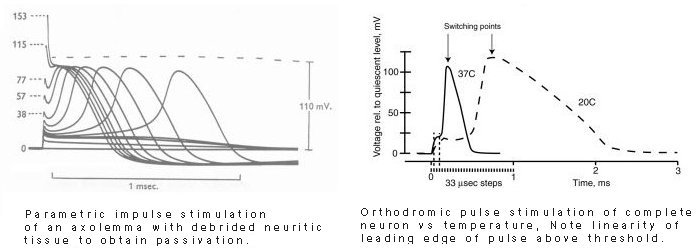
There are major differences between these two groups of waveforms. The Hodgkin et al. waveforms are;
The Schwartz & Eikhof waveforms are quite different;
The literature contains many recordings of Action Potentials similar to those of Schwartz & Eikhof.
The Hodgkin & Huxley waveforms do not represent Action Potentials under the current definition of that term.
Attempts to create computational models of Action Potentials based on the Hodgkin & Huxley waveforms may be a useful pedagogical exercise for entry level students, but they have little utility in academic research.
The responses to parametric stimulation using impulses (provided by Hodgkin & Huxley) can provide information as to the configuration and values of circuit elements within the test configuration (including the axolemma within that configuration) using standard network realization techniques of electrical engineering.
The previous paragraph, those preceding it in this section, and the many other detailed problems with the Hodgkin & Huxley model summarized in the literature support the need for a new functional model of the complete neuron. Frankenhauser & Huxley summarized, in 1964, many of the problems with the H & H model of the axon (as well as its extension to the neuron). Those authors explore fifteen distinct aspects of the previously proposed differential equations (A primary equation with approximately 16 auxiliary equations). As an example: "(15) It has not been possible to carry out a complete analysis on one single fibre; different parts of the data refer to different fibres." They go on to say "The equations and the quantitative data obtained in the voltage clamp analysis must to a large extent be considered as approximations. A fair amount of scatter appears especially between values from different fibres. The equation system is so involved that it is impossible in most cases to get even a fair idea of the effect of a change of a single value without going through a complete computation."
Clay reviewed and reiterated the Hodgkin paper of [xxxfrom appendix x ]
Clay & Schrier made an additional finding in 2001. Even with an axial wire inserted in the axolemma, the giant axon of squid was susceptible to spontaneous action potential generation. They also introduced a different form for the equation for INa; it dispensed with the n4 term in favor of fewer but still multiple exponential functions with individual time constants.
After recapitulating the type definitions of Action Potential generators of Hodgkin (1948) in 2008, Clay et al. asserted,
"Type 3 axons fired at most once or twice, or not at all regardless of stimulus intensity or duration. Squid giant axons exhibit type 3 excitability which is surprising since the Hodgkin & Huxley equations of this preparation describe type 2 behaviour."
They then modified their model to account for this fact. Their new model includes even more individual coefficients than earlier models, a nearly overwhelming number.
In their discussion, following their conclusions, Clay et al. make the following points;
The distinction between signal propagation and lumped component signaling attributed to a "local circuit" mechanism by Hodgkin & Huxley (Hodgkin, 1951, page 389) is now recognized to be a clear manifestation of Maxwell's General Wave Equation applied to a myelinated axon segment. There is no mechanism to support the movement of sodium or potassium ions through the combinaton of a lemma within a tightly wrapped myelin overlay as suggested by H & H.
- - - -
In the 1940's, Hodgkin, then Hodgkin and Huxley, and then Hodgkin, Huxley and Katz addressed the dynamics of the neuron as they understood it. Their generic neuron consisted of a single active chamber surrounded by an axolemma. The assumption was that the axolemma itself must be the active element. Hodgkin attempted to develop a cursory dynamic theory in 1949 based on his work with crustaceans. Hodgkin and Huxley reported on extensive laboratory investigations on the "giant axon" of the squid, Loligo in the 1950's. In hindsight, their work suffered from a variety of shortcomings that still plague the community today. The chemical aspects of these problems are addressed in a separate document, the Falsification of the Chemical Neuron based on the diffusion Laws. The problems associated with computational modeling of their framework are addressed below.
Initially, Hodgkin and Huxley only discussed inward currents and outward currents in their attempts to describe the operation of the neuron. They later used the euphemisms, inward sodium current and outward potassium current in accordance with the prevalent beliefs. With their widely heralded work, these labels were shortened to the sodium current and pottasium currents (and others) without any consideration of the role of electrons in electro-chemistry (and without recognition of Benjamin Franklin's error in assuming positive charges flowed from the positive terminal of a battery through an external circuit to the negative terminal. The fact is the only electrical current flowing within an electro-chemical environment is the electron charge flowing from the negative terminal to the positive terminal of a battery. It is this charge flow that is measured in all laboratory environment not involving quantum-mechanical semiconductors. A pseudo-positive charge flow (hole current flow) does exist in quantum-mechanical semiconductors but this was unknown until the 1950's. Quantum-mechanical semiconductors do include (including many molecules and specifically liquid crystalline molecular species.
Baxter & Byrne analyzed the record related to the H & H framework describing the operation of the neuron in detail. They also reviewed some of the related activities under way at that time. They described the framework specifically;
They did not note that the values of four and three for n and m were totally arbitrary and could have just as well been raised to five or six and four or five. They described some of the limitations on the framework (page 197), offered their version of the list of parameters required to use the framework, introduced a term related to temperature into the H & H equations, and offered a simplified set of equations for the action potential (page 199). They also introduce a "phase plane" analysis of action potential generation based on their simplified set of equations. Their phase plane is not that of electrical engineering, but an arbitrary plotting of one uni-dimensional dependent variable against another, with time as the independent parameter. The utility of their phase plane analysis is yet to be demonstrated.
The temperature term introduced by Baxter & Byrnes was totally empirical and was applied to all aspects of the differential equations. It was based on the number 3 raised to a power given by (T-6.3)/10. The value of 6.3 Celsius was assumed to be the standard temperature used by H & H and the factor 10 is suggestive of a biological temperature range narrower than the Arrhenius range given in degrees Kelvin.
Baxter & Byrne also review several alternates, labeled reduced models, to the H & H framework (page 211).
After several hundred pages of material, Hodgkin & Huxley suddenly attempt to introduce the quantum-mechanical model known as Boltzmann's Principle on page 503. Boltzmann's principle is usually expressed using the Boltzmann Distribution Law. This principle is normally used to explain the distribution of electrons among the allowed energy states of a material at the atomic level. It is also valuable in discussing the distribution of particles in an ideal gas. Their adoption of this principle to explain the distribution of "special charged molecules" between the two surfaces of a membrane (of totally unspecified character) appears to be unique. No other application of this principle in this manner, separate from that to an axolemma, could be found in the literature.
H & H introduced three equations on page 503 that do not carry sequence numbers like the other equations in the paper. The relationship between the equations is muddled. The second equation includes a minus sign that is not derivable from the first equation. In addition, the third equation depends on the fact that "w, the work required to move the molecule from the inside to the outside of the membrane when E = 0," is negligible. For a continuous bilayer lemma, the value of w is now known to be quite large (Section xxx of N&NS). The only way to make w negligible is to introduce another pathway through the lemma that is independent of its normal amphophilic structure, typically a conceptual pore.
Because of the minus sign introduced into equation two, and the assumption that "For negative values of z, and with E sufficiently large and positive," the value of Pi grows without limit as E increases in the third equation, necessitating the introduction of an undefined "constant" to force Pi <1.00.
If the errant minus sign is eliminated from the second equation, the third equation assumes a different form "for negative values of z and large values of E, and does not require introduction of the arbitrary constant. If a suitable path is introduced that exhibits a w that is negligible (such as a pore through the lemma), the equation becoomes the conventional probability equation for a two-choice Boltzmann Distribution,
Pi = 1/[1 + exp((zeE)/kT)]
For negative values of z, this equation gives;
Pi = 0.5 for E = 0 and Pi = 1.00 for large values of E.
With the above corrections, the remainder of the discussion in Part 1 of the paper are irrelevant, except for their interesting statement, "Details of the mechanism (operation of the putative pores) will probably not be settled for some time,"
After more than sixty years of intense laboratory research, no "special charged molecule" present on the outer and inner surfaces of the axolemma has been found corresponding to their proposal on page 503. While contemplations related to such a molecule may have contributed to the concept of a port or channel through the axolemma, no structures related to these ports or channels have been identified in the laboratory to date. However, descriptions of such putative molecules has proliferated in the modeling community. Lacking such special charged molecules, the working hypothesis of Hodgkin & Huxley related to the fourth power in the equation (#26, page 518 based on #6 & #14) describing the conductances of sodium and potassium must be discarded.
The ad hoc adoption of Boltzmann's Principle by Hodgkin & Huxley is emphasized by their assertion that raising the unit-less expression for conductivity from the fourth to the fifth or sixth power might provide a better fit of the equation to their data.
They conclude on page 504 that their special charged molecule requires a net electrical charge of -6; or they suggest it might be formed by a complex of six molecules of -1 electrical charge.
These ideas, based on the Boltzmann Principle, have been pursued intensely within the computational community and have led to the idea of pores and gates (Baxter & Byrne) but they have been pursued less successfully in the biological community where pores and gates have not been identified. Nor has any equivalent circuit or mechanism been identified approximating the Hodgkin & Huxley proposal.
As late as 2009, Baxter & Byrne chose to reproduce an action potential from the H & H paper of 1952d which is clearly not a complete action potential; and show that their interpretation of the H & H equations provides an accurate simulation of that recording. The cited action potential does not show any axon threshold level, nor the linear amplification of the stimulus waveform at voltages below the threshold level (See the above waveform of Schwartz & Eikhof, 1987).
Hodgkin & Husley did not offer a physical or chemical model of their neuron. They only compiled a set of partial differential equations that could be manipulated to represent an action potential generated from their descriptive text.
The neuron described by Hodgkin and Huxley, and their proposed first order mathematical description of the action potential generated by it is testable (falsifiable) to a degree but relies a great deal on the readers mathematical training and intuition as well as his biological training.
The model of Hodgkin & Huxley outlined above has been shown to be in conflict with the experimental facts. These facts are reviewed below. The original, and unstated, null hypothesis of Hodgkin and Huxley; that the debrided and parametrically stimulated axolemma of a locomotion neuron of a member of Mollusca, the squid Loligo, faithfully represents the Action Potential described by recordings of the orthodromically and pulse stimulated stage 3 neurons of Chordata is refulted based on the empirical record.
As shown on an associated page, the null hypothesis that the axoplasm potential of a neuron is established by the relative concentrations of the alkali and alkali earth ions on opposite sided of the axolemma is refulted based on the experimental record showing the presence of sodium is not required in the extraneural matrix for normal neuron polarization.
Figure at end of page.
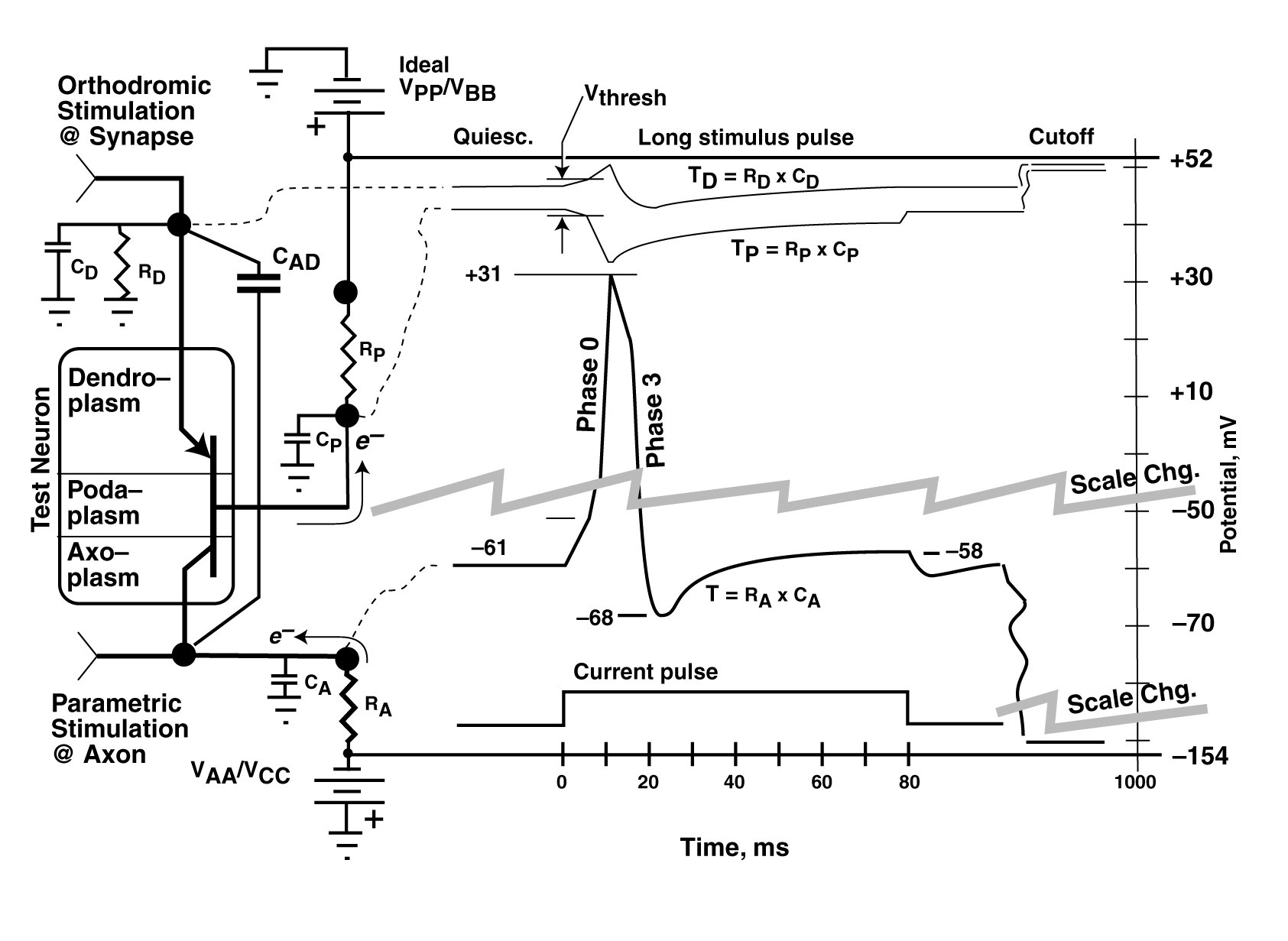
It is difficult to disparage the experimental results of those working more than 60 years ago with the technology of their time. However, there appear to be questions concerning the operating protocols and the instrumentation used by Hodgkin & Huxley to acquire their data. This section should be looked upon as an attempt by this author to understand their test protocols and instrumentation.
Hodgkin & Huxley struggled mightily with the relevant electro-chemistry in their 1952a paper. The struggle led to their assertion of their independence principle (page 467) which generally conflicts with their prior reliance on the diffusion laws of Nernst, then Donner and then Goldman. This principle has never been confirmed or reasserted by others. Twenty-four years later, Barrow noted, "A better understanding of the ionic world than we now have would be necessary" to explain the mobility of mixtures of solvated ions and the resultant current partitioning.
They offered no null hypothesis prior to their investigations or their discussion concerning their measurements. Only a null hypothesis based on logic can be drawn up at this time. It appears, they assumed;
As noted above, Hodgkin & Huxley defined a term, "chord conductance" based on the data reported in figures 9 and 10 on page 464. These chord conductances were obtained as the peak values obtained in voltage clamp experiments depolarizing from the quiescent potential of their test configuration. As they note when comparing the curves for sodium and potassium conductance, "The two curves are very similar in shape." In fact, they are identical within the precision of their measurements.
It is important to recite four definitions of the term conductance as used in different contexts.
Hodgkin & Huxley were measuring electrical currents in their voltage clamp experiments which they attributed to the flow of either sodium or potassium only through their membrane. It is more likely that the dominant flow of charges was due to the flow of electrons rather than alkali or alkali-earth ions, particularly since electrons have a significantly higher mobility within membranes compared to alkali or alkali-earth ions. In solutions, the mobility of both electrons and H3O+ are much higher (3x to 7x) than that of sodium and potassium ions. As noted above, the mobility of electrical charges within biological membranes is thousand to millions of times higher than for the ions of sodium and potassium.
They measured the maximum total current as a function of the change in clamp potential and divided this change in current value by the change in clamp potential to obtain their chord conductance, g = DI(V)/DV. An alternate approach is to recognize their changes in total current were a function of the change in voltage, DI(V) and attempt to determine the origin of that function, . By inspection, the curve is derived from that of a perfect diode given by the equation,
I = I0(eV/hVT - 1)
In its more sophisticated form, the potential, V, should be replaced by V- Vg where Vg is the cutin voltage. A reliable value of h for type 2 biological membranes remains unknown at this time. It varies between 1 for germanium and 2 for silicon devices but may vary marginally with manufacturing procedure.
Hodgkin & Huxley describe their method of obtaining their "chord conductances" on page 463. It involved a complex evaluation of transient waveforms that they did not describe explicitly. As they note, their sample sizes were quite small and "the sodium conductance is probably steeper than that of the potassium data." They describe their slopes as an e-fold increase for 4 mV in the case of sodium and 5 mV in the case of potassium. Note a one digit accuracy but no indication of the precision of these numbers.
The following figure shows their original figures 9 and 10 with the upper figure overlaid by the above equation for a perfect diode (red line). It is important to notice that Hodgkin & Huxley omitted any units from their description of the ordinate, which they defined in the text as the permeability of the membrane to the specific species of ion. Note also the ordinate scale is a relative scale, it is relative to the maximum reached with 100 mV depolarization.
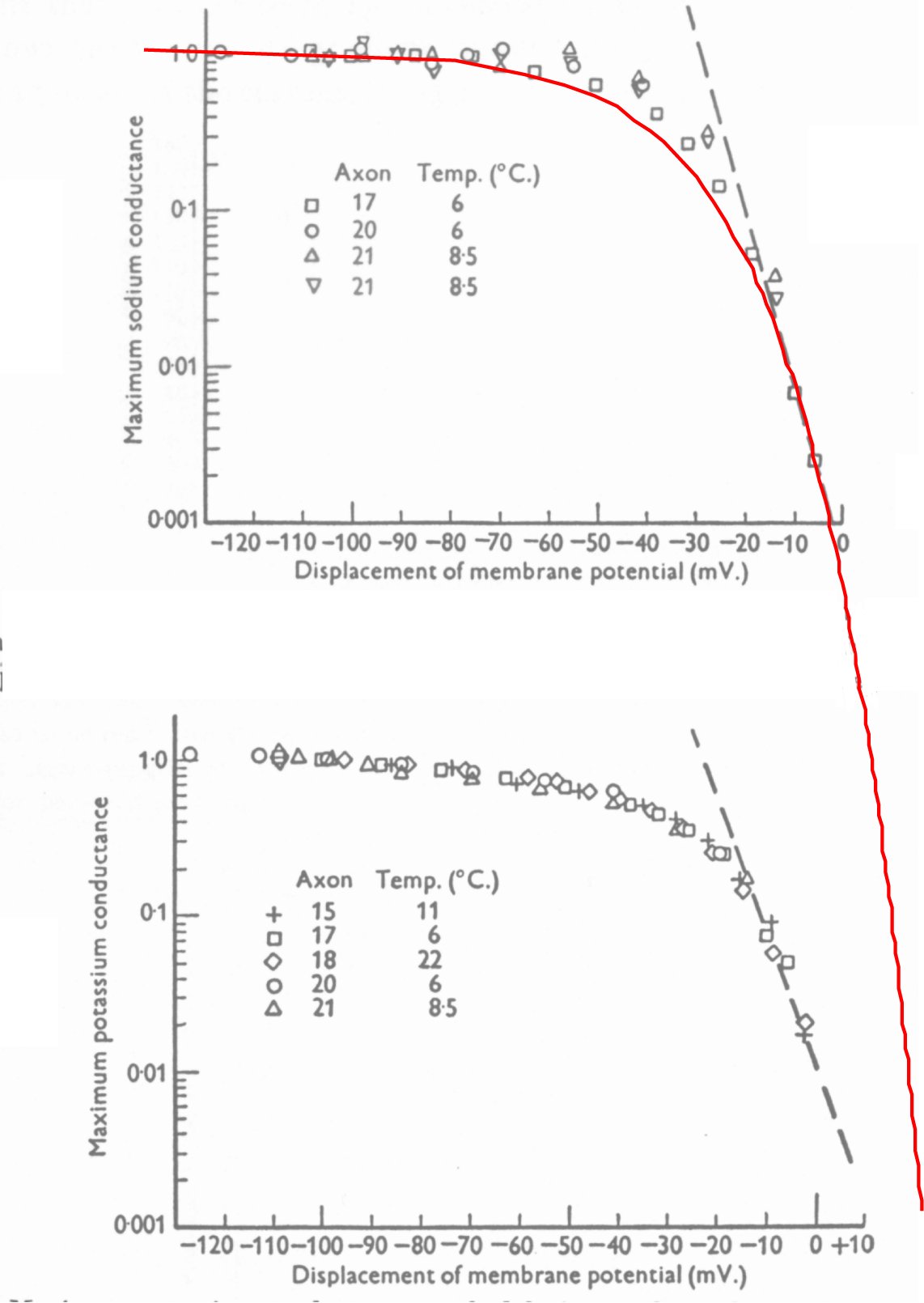
The reader can manipulate the upper figure attributed to sodium and the lower figure attributed to potassium off-line to demonstrate they overlay each other just as Hodgkin & Huxley noted. There is no statistical difference between the two functions based on the choice of sodium or potassium in the solution. It is proposed these two sets of data are dominated by the same lurking mechanism, unrecognized by Hodgkin & Huxley, the dominance of the higher mobility of electrical charges compared to ions within their membrane.
The red line displays the electrical current (on a linear scale) as calculated for an ideal semiconducting diode at 280 Kelvin or 7 Celsius over a potential range of 150 mV with h = to 1.0 and Vg = to 0.00. Using different values for these two parameters, the curve can be adjusted to matches the data points for axon 17 arbitrarily well. The precision of the laboratory experiments does not justify this additional effort. The horizontal position of the diode curve is arbitrary, since Vg is note known and the data is not precise enough to provide a value. Note how the slope of the red line continues to change as it falls. It shows that the slope of the data points depends on where you measure them. The change in potential required to achieve an e-fold change in the ordinate will also change with location of slope measurement. Adjusting the parameters of the diode equation demonstrates that the measured curves for different temperatures are different and should not be averaged.
- - - -
Hodgkin & Huxley also struggled mightily with their test electronics in their 1952a paper. They presented their electrical instrumentation in abbreviated form (fig 6) on page 430. Their discussion is of interest. No explanation was given why they exceeded the maximum plate-to-cathode potential for the 6AK5 vacuum tubes by a factor of over 200%
They defined a compensated feed-back condition that they used for most of their experiments. It is doubtful that they appreciated the fact their instrumentation consisted of a position control servomechanism with two distinct error sensing inputs. They noted on page 431 that the circuit exbited only marginal stability, and discussed the fact that the uncalibrated rheostat had to be set to a value of p = 0.6 or less. If the value was higher, they note, the overall feedback became positive and membranes were frequently destroyed. This wording may be poor; it may be that "the overall feedback factor became greater than 1.0 and membranes were frequently destroyed." They made it clear on page 445 that the overall circuit exhibited a "polarization effect" that they could not account for. The effect is clearly due to the lead network associated with the capacitor C. It has a calculated time constant of 33 milliseconds. This long time constant makes their instrumentation operate like an AC coupled system for pulses of the short duration used. Their observation that the loop gain of their feedback loop was nominally 400 but was as high as 1200 under transient conditions is critically important. The change in gain is clearly due to the lead network of C1 and the two associated resistors. These comments suggest the test configuration with compensated feed-back exhibits unstable negative transient feedback and stable long term negtive feedback stability. A root-locus analysis of this circuit would suggest it is highly unstable at loop gains above 450 for p = 0.6. They provided figure 17 on page 446 to explain the operation of their system with and without feedback using axon 34. It is obvious that the interpretation of the specific waveforms of their paper are critically dependent on whether the uncompenasasated or compensated feedback configuration was used during data collection. The above observations are compatible with their figures 10 through 14.
Figure 13 introduces another problem with Hodgkin & Huxley's method of analysis. When using compensated feedback, The transient (marked A) in figure figure 13 on page 439 is compatible with the current waveform of figure 17 (beta). However, the line labeled "steady state" in their text, is far from that. It is labeled "Not Steady State" in the reproduction below. It is actually a hybrid with the values reported for a given current taken at different times (given by the labels in milliseconds) in the transient response of the waveforms collected for different voltage changes. This mislabeling can significantly mislead an analyst attempting to use their data.
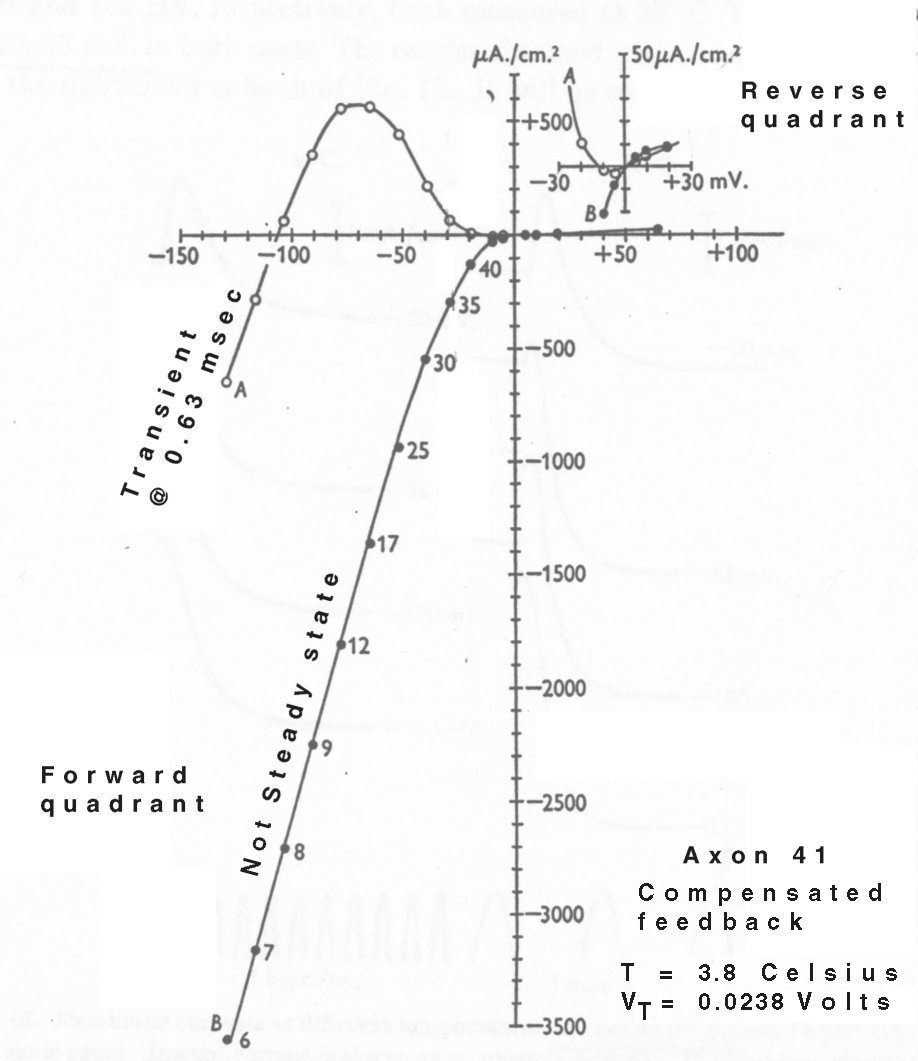
The reported "steady state" response of their membrane is suggestive of a typical biological diode with data points in the first and third quadrants. However, the use of points acquired at different times from a set of transient responses to different voltage clamp levels defies further analysis.
The reported transient response data does not suggest a simple physical model, except to note the presence of a negative slope in a waveform in the second quadrant indicates a negative resistance (an active source) is present.
Hodgkin & Huxley also struggled mightily with the equivalent circuit (page 501) describing their working hypothesis in their final 1952 paper. They define two variable impedances and describe them using the symbol for a resistive element. This symbol is universally associated with a resistor in conformance with Ohm's Law. Such a resistor is independent of the current passing through the resistor or the voltage applied to the resistor. It is also implicitly independent of the variable time. However, the variable impedances of Hodgkin & Huxley are both functions of both voltage and time. Their described impedances are not electrical circuit elements known to the electronics community. An alternate symbology must be used to avoid misleading new students entering the field.
The equivalent circuit on page 501 also lacks the two ion pumps required to return the axolemma environment to its pre-pulse quiescent chemical concentration environment.
The null hypothesis attributed to Hodgkin & Huxley earlier in this section can be refuted based on our current knowledge. This knowledge provides an alternate null hypothesis for future investigation.
It is proposed here that their data points relate to the static total current (dominated by the electron current) through all of the type 2 axolemma remaining from the debriding of the pedicles of their axon, as a function of the potential across the axolemma. The type 2 axolemma forms a perfect diode based on the flow of electrons (or the equivalent holes generally associated with H3O+) along its asymmetrical bilayer phospholipid structure. This proposal can be easily confirmed or refuted using simple static test procedures. During such tests, it is important that the temperature be controlled to better than 0.5 Celsius if statistical methods are to be employed in data reduction. For accuracy, a Ussing type test cell should be employed rather than the simpler electrolytic cell of textbooks. The Ussing test cell allows the determination of the conductance of the fluids used to bath the biological membrane, another lurking variable in the report of Hodgkin & Huxley. The difference in maximum conductivity in figures 11 and 12 of Hodgkin & Huxley suggest their solutes exhibited different conductivities (note conclusion #3 on page 471).
Those interested in pursuing computational modeling of a neuron, or of incorporating such modeling into a larger model of the neural system based on the working hypothesis of Hodgkin & Huxley should be aware of its limitations.
The best available description of their last working hypothesis, based on their concept of pores or gates in the largely benign axolemma, was developed above. The hypothesis is;
Hodgkin, A. (1948) The local electric changes associated with repetitive action in a non-medullated axon J Physiol vol I07, pp 165-181
Hiodgkin, A & Katz, B. (1949) The effect of sodium ions on the electrical activity of the giant axon of the squid J Physiol vol 108, pp 37-77
Hodgkin, A. (1951) The ionic basis of electrical activity in nerve and muscle Biol Rev Cambr Philos Soc vol 26, pp 339-409
Hodgkiin, A. Huxley, A. & Katz, B. (1952) Measurement of current-voltage relations in the membrane of the giant axon of Loligo J Physiol vol 116, pp 424-448
Hodgkin A. & Huxley, A. (1952) a series in the J Phisiol , (1952A, vol 116, pp 449-472), (1952B, pp vol 116, 473-496), (1952C, vol 116, pp 497-506) and (1952D, vol 117, pp 500-544)
Barrow, G. (1966) Physical Chemistry, 2nd Ed. NY: McGraw-Hill page 680.
Baxter, D. & Byrne, J. (2009) Dynamical Properties of Excitable Membranes In Burne, J. & Roberts, J. eds. From Molecules to Networks 2nd Ed. NY: Academic Press Chap 7, pp 181-203
Clay, J. & Shlesinger, M (1983) Effects of external cesium and rubidium on outward potassium currents in squid axons. Biophys J vol 42, pp 43–53
Clay, J. (1998) Excitability of the squid giant axon revisited J Neurophysiol vol 80, pp 903-913
Clay, J. & Schrier, A. (2001) Action potentials occur spontaneously in squid giant axons with moderately alkaline intracellular pH Biol. Bull vol 201(2), pp 186-192
Clay, J. Paydarfar, D. & Forger, D. (2008) A simple modification of the Hodgkin and Huxley equations explains type 3 excitability in squid giant axons J R Soc Interface vol 5, pp 1421–1428
Cole, K. (1968) Membranes, ions and impulses. Berkeley, CA: University of California Press, pp 60+
Frankenhaeuser, B. & Huxley, A. (1964) The action potential in the myelinated nerve fibre of Xenopus laevis as computed on the basis of voltage clamp data J Physiol vol 171, pp 302-315
Fulton, J. (2004) Processes in Biological Vision. Chapter 10, Part II and Appendix X in neuronresearch.net/vision/document.htm. APPENDIX NOT YET POSTED.
Fulton, J. (2010) Neuron and Neural System Processes. Chapters 4 in neuronresearch.net/neuron/document.htm
Glasoe, G. & Lebacqz, J. (1948) Pulse Generators; volume 5, Radiation Laboratory Series. NY: McGraw-Hill, pp 124-125
Gray, T. (1954) Applied Electronics. NY: John Wiley & Sons pp 819-825
Return to the Neuron Research home page.