
This Appendix is limited to a superficial review of the current field of colorimetry and its application (and shortcomings when applied to) vision. Many important points are surfaced at the philosophical level. This leads to an expansion of the concept of colorimetry that is fundamental to the study of color vision.
R.1.1 Historical perspective
Colorimetry as an element of artistic works has existed for a long time. However, its development into a science awaited the development of practical photo-electronic measuring devices. This only occurred in the late 1920's and 1930's. The fields of colorimetry and photometry developed essentially in parallel. The lesser known field of radiometry, which is the parent of both colorimetry and photometry developed somewhat later. Because of this inversion, the theoretical foundations of these fields is suspect and somewhat poorly defined. In many cases, the psychophysical community has chosen to employ various photometers and colorimeters without defining the precise capabilities of these instruments. This has left the data difficult to interpret within a larger milieu of data. The field has also suffered from a lack of clear definition of the fundamental term color. In this work, it has been found necessary to define color in a situational context. The result is a series of definitions of color involving a number of single word prefixes. One of the few comprehensive discussions of colorimetry appears in Chapter three of Wyszecki & Stiles (1). Unfortunately, their presentation suffers substantially from the lack of a theoretical base and begins with the empirical generalization known as "the trichromatic generalization. The Chapter is based entirely on linear additive color concepts and the "color equation" of conventional wisdom (their equation 1[3.2.2]).
Early photometric investigations employed comparitive techniques, generally employing two channels of light presented in a bipartite arrangement and using the human eye as a null detector. This was at best a poor choice because of the various spectral characteristics involved. If a common light source was used to generate the signal in both channels, the instrument was no longer a photometer but more properly a reflectometer or transometer. If separate light sources were used, the question of the color temperature of the individual sources was generally not addressed scientifically (in terms of color temperature or some other spectrally explicit nomenclature). Usually the reference source was described by its general construction and the voltage and current applied to it. It was unusual before the late 1930's to be concerned with the spectral impact of the envelope used in the construction of the light source.
Only with the advent of electronics was it feasible to develop sophisticated sensors that were designed to mimic the characteristics of the human eye while providing a direct measurement of the spectrally integrated power received from a light source or reflected from a scene. In modern times, most photometry and colorimetry are described using direct reading instrumentation.
Workers in the field have long recognized the importance of what is generally defined as additive and subtractive color mixing. When individual chromatic sources of light are mixed, the color of the resulting light is generally described as an additive process. On the other hand, when a light is reflected by a surface or transmitted through a filter, the color of the resulting light is generally described as a subtractive process. Unfortunately, the description of the actual spectral characteristics of the lights and materials involved is frequently unknown. The result frequently leads to inconsistent and less than reproducible results between experimenters.
This latter problem is particularly severe due to the lack of precise semantic definition of particular colors. Various color names are used that do not indicated the spectral quality, particularly spectral width, of the particular color being described. The shape of the spectral characteristic is particularly important when speaking of the terms, violet, purple and magenta.
R.1.2 Conventional scientific description of colorimetry
R.1.2.1 Colorimetry as a field of radiometry
Colorimetry has developed as a specialty within the field of photometry, which is itself a specialty within the field of radiometry. Although radiometry first developed as a phase in the development of radio, it is not limited to the spectrum used by radio waves. The concept is broader, a radiometer is a meter for measuring radiation, not radio waves. Because of the expanse of the radiation spectrum, many decades in width, it is difficult, if not impossible, to build a single radiometer capable of operating over the entire spectrum. Therefore, it is common to find radiometers designed to operate in the long wavelength, or radio, spectrum, the microwave spectrum, the infra-red spectrum, the visual spectrum, and even the ultraviolet spectrum. Most radiometers are designed as broadband meters. Their response, either inherently or through calibration, is meant to be constant for a constant radiant intensity across their operating spectrum. This intent is complicated by the width of the radiometric spectrum. Because of this width, and the question of investigative convenience, it is common to design these instruments to exhibit a constant response as a function of frequency up through the microwave spectrum but as function of wavelength from the infrared through ultraviolet region of the spectrum. Since frequency and wavelength are reciprocal to each other, this introduces a distinctly different characteristic to these meters.
R.1.2.2 The Quality Factor in radiometry
This difference also makes the definition of the relative width of a given spectral source, or of a given spectral filter, difficult. Below microwave frequencies, the quality factor, Q, of a filter or source is usually described in terms of its center frequency divided by its spectral width measured between its half-amplitude power points . A similar calculation can be made based on wavelength. However, the value obtained is obviously different. Some method of notation is required to separate the Q based on frequency from the Q based on wavelength.
In the past, the calculation of the Q of a visual band signal has not been used. In many cases, the Q is not a useful measurement because of the complex spectral characteristic of a source or a material. However, it has become important in this work in the definition of the spectral performance of the chromophores of vision. When discussing the Q of the quantum mechanical process fundamental to the spectral response of the chromophores, it could be expected that very similar chromophores would exhibit similar Q's. However, it is not obvious at first glance whether such similarity should be based on wavelength or on frequency. It appears that the use of a quality factor based on wavelength is more appropriate.
R.1.2.3 The complexity of the quantum nature of radiation
Besides the change in baseline, between frequency in the case of radiometers used at frequency below the microwave level and wavelength in the case of higher frequency radiometers, there is another fundamental difference. Within the spectrum including the infrared and lower frequency regions, the primary characteristic of radiation is the total energy associated with it. This is the area of heat sensitive measuring devices. In this area, it is common to think of the intensity of radiation in terms of energy units and a source is frequently described as exhibiting a constant output energy per unit frequency. This is a misnomer since the typical parameter is the power per unit frequency, i. e., the energy per second per unit frequency.
At frequencies above the infrared region, it is important to recognize the quantum nature of radiation. For many detectors in this region, power (or energy per second), is not the relevant parameter. The relevant parameter is the number of quantum absorbed by the detector per second, regardless of the energy of those quanta (or photons). This important differentiation was formalized by Einstein in his description of the Photoelectric Effect in 1907.
Because of the Photoelectric effect, it is important to define whether a given radiometric detector senses power or quantum flux.
R.1.2.4 The definition of a photometer
Initially, a radiometer designed to cover the expanse of spectrum related to the visual capability of animals might be called a visualometer. However, for historical reasons it became known as a photometer. This occurred in a time period when other types of photons were unknown or poorly understood. The initial assumption could be made, based on its radiometric ancestry, that a visualometer or photometer would be a broadband device providing a constant output for an input signal of constant radiometric intensity. However, because of its limited theoretical past, the current photometer developed along different lines. It was designed to provide an output directly related to what the human eye sensed (in a completely undefined manner). Such an instrument evolved to include a filter representative of the photopic response of the human eye. Later, models appeared that also included the option of a filter representative of the scotopic response of the eye.
The detector in early photometers was always a power sensing device (dependent on the heat related characteristic of the incident radiation). When higher sensitivity photometers became necessary, detectors based on the photoelectric effect were introduced into these devices. Since they were not power sensitive devices, a compensating filter was introduced--or combined with the previous photopic or scotopic filter. The result was a photometer that still provided an output reflecting the total incident power (energy per second) integrated over the photopic or scotopic spectral band.
The precision with which these instruments duplicated a particular prescribed photopic or scotopic spectrum was, and is, usually not specified in detail. The question of whether a true photometer designed to emulate the human eye in some way should be a power meter or a quantum flux meter has probably never been addressed. It will be below.
R.1.2.6 The definition of a colorimeter
The development of colorimeters has followed a similar path to that of photometers. Early units were comparators with the human eye used as a null detector in the matching process. Later units, easier to use and therefore more widely used, were direct reading instruments.
The comparator procedures generally followed the Young concept that any color could be matched using three well differentiated lights. An alternate procedure, that any light could be matched using a white light and one other, was simpler but failed when attempting to match colors in the "purple" region. These were defined as non-spectral colors.
R.1.2.7 The definition of a direct reading colorimeter
With the direct reading photometer defined along the lines described above, it was natural to attempt to define a direct reading colorimeter
In designing a direct reading colorimeter, the concept generally followed was that any light sensing system was governed by the light falling on the detectors and it should therefore be designed based on additive colorimetry rules. The general rule has been to segregate the visual spectrum into three separate channels. Each of these channels employs a spectral filter matching one of the putative spectral absorption characteristics of the visual pigments. By recording the values recorded by the individual channels of the direct reading colorimeter, the "color" of the input signal could be quantified. These values could be algebraically summed as in the traditional color equation to give an equivalent intensity value. Alternately, they could be related to a chromaticity type diagram. Unfortunately, the values reported by a direct reading as described is entirely dependent on the light source used. The readings will vary with the color temperature, or detailed variation in the spectral emission, of the light source.
By mathematical manipulation, these values can be converted into coordinates on the C.I.E (1931) Chromaticity Diagram (or one of its progeny). The description of the chromatic characteristics of the eye based on this procedure have not been widely disseminated, leading to the conclusion that the results have not been widely accepted as satisfactory. Only one figure could be found in the literature that attempted to specifically identify "colors" with a coordinate system similar to that of the C.I.E. Chromaticity Diagram. This was by Dean Farnsworth and applied to a Deutan (2).
R.1.3 Additive versus subtractive colorimetry
The conventional wisdom has been that at least the human visual system, if not all animal systems, relies upon linear additive colorimetry. However, this has never been demonstrated. The corollary assumption has been that a single equation, of the color equation type, Q=rR + gG + bB or Q= sS + mM + lL, properly represents the performance of the visual system in object space. This has never been demonstrated either.
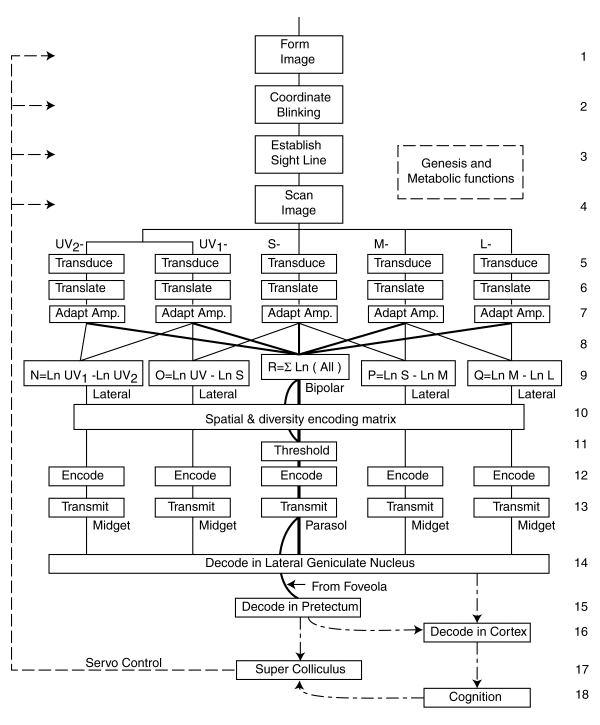
If one looks at the functional block diagram of the human visual system, it is clear that the above assumptions are poor ones.

Functional Block Diagram of the animal visual system. Ref. [11.6.3-1]
The luminance channel, R, does involve a summation of the signals from the individual spectral channels. However, the summation is in logarithmic, and not linear, space. Counter to this summation process, the two chrominance channels, P & Q, employ subtraction in logarithmic space. This process effectively finds the logarithm of the intensity ratio between pairs of spectral channels at the pedicel.
Since both the logarithmic summation in the luminance channel and the logarithmic differencing in the two chrominance channels occurs after the adaptation process, the resulting signals have little relationship to the absolute intensity level of the scene. Furthermore, the ratios defining the chromatic aspects of the scene have no direct relationship to the incident luminance level, normally given by the symbol Y in photometry but usually given by Q in colorimetry.
This situation is not compatible with the conventional wisdom that the performance of the visual system can be described using linear algebraic summation. The concepts used to create the conventional chromaticity diagram are basically untenable.
R.1.3.1 New definition of "WHITE"
Recognizing the colorimetry of vision is more properly described using subtractive colorimetry, several new definitions are appropriate. The most important is a new definition of "white." It is important that such a definition be fundamental at both the conceptual and scientific levels and that it reflect the fundamentally perceptual aspect of the phenomena. It appears that such a definition would allow one definition that would apply under all illumination conditions and to color abnormals (color blind) as well as normals.
Based on the visual system block diagram, it becomes clear that there is a unique condition that leaves the visual system operating in an achromatic mode. The condition is obtained when the value of the perceived signal in each of the chrominance channels is null. For a long wavelength trichromat, this condition is given by the condition; R:P:Q::R,0,0 regardless of the nature of the incident illumination.
The condition R:P:Q::R,0,0 appears to be the condition of the fully dark adapted eye for very low levels of R. It also appears to be the normal condition when the eye is excited by a source of equal flux radiation per unit wavelength, such as a black body source of 7053 Kelvin. The precision of this assumption requires detailed laboratory verification.
Based on these fundamentals, a definition of the color white can be given as;
"White is the reported color, of a light or an illuminated surface, perceived by an animal when each and all of the chrominance channels of its visual system are reporting a null condition to the cortex for that incident illumination. For a long wavelength trichromat, this condition corresponds to a null in both of the chrominance channels, P:Q::0:0"
The above definition is independent of the state of adaptation of the animals eye and of any short term flicker type phenomena. To express the definition of white in object space, it is necessary to know the state of adaptation of each of the spectrally sensitive photoreceptor channels, the absorption characteristic of the physical optics of the eye, as well as the temporal character of the illumination received at the cornea.
R.1.3.1.1 Color constancy as a result of adaptation
Under the above definition, an animal will report an object in object space as white if all of the chrominance channels are each reporting a null signal. This can occur for any eye under a variety of conditions. Looking only at steady state conditions, it can occur under two distinct classes of conditions;
+ when all of the adaptation amplifiers are operating at their quiescent gain, there is no significant spectrally selective absorption within the physical optical system of the eye, and the spectral content of the illuminance received at the cornea is nominal.
This nominal condition is believed to be an illuminance that exhibits equal quantum flux per unit spectral interval across the spectrum of interest. It is proposed that this nominal condition is achieved using a 7053 Kelvin color temperature light source. If the eye is illuminated by reflection from a surface, the spectral characteristic of the illumination incident on the eye must be of this spectral character.
+ when the intensity of irradiance in one of the spectral channels is greater or less than anticipated relative to the other spectral channels, and the adaptation amplifier associated with that channel adjusts its gain to compensate for this abnormality.
This process of compensation is the basis for the phenomena known as "color constancy." As a result of this compensation, the null conditions prescribed for reporting of "white" within the visual system proximal to the pedicels of the photoreceptors are not reflected into object space as requiring the same ratio of intensities between the three spectral channels of the system.
R.1.3.1.2 Elimination of the deconvolution problem
On the assumption that the visual system is a linear system, the literature contains a large number of papers attempting to explain color constancy in a variety of terms (some quite ephemeral). Many of these papers do not include a clear definition of the terms color and white; even conceptually. Because of the assumption of linearity and the failure to define color specifically in object space, these papers frequently take the position that the spectral reflectance of an object does not represent its color in a unique manner.
These papers, therefore, assume that the visual system determines the intrinsic color of an object through some complex calculation designed to separate the intrinsic spectral reflectance or transmission characteristics of the object from the spectral characteristics of the light incident on the object.
Recognizing the ability of each spectral channel of the visual system to change its gain dynamically with a time constant on the order of a few seconds, and that the common reference point for these gain changes is the availability of electrostenolytic supplies to the affected group of photoreceptors, an entirely different explanation of the color constancy phenomena is available. Color constancy is the phenomena observed due to the ability of the individual spectrally selective photoreceptor channels to change their gain, relative to the associated channels, in response to a slowly changing level of irradiance. The result is a movement of the white point in object space relative to its spectral location in perceptual space. This phenomena can result in an apparent constancy of the color of surfaces in object space as long as the adaptation amplifiers of the spectral channels are all operating within their normal amplitude operating range.
Under this interpretation, the subject of deconvolution of the incident illumination to calculate the spectral characteristics of the surface in question is unnecessary.
R.1.3.1.1 "WHITE" as perceived by the color abnormal
The above definition of white is completely applicable to any color abnormal at the perceptual level. The propagation of this definition back through the visual system to object space also gives a unique definition of object white applicable to a specific class of color defects. It also provides a simple explanation for the apparently similar performance of the two classes of "red-green" color-blind individuals.
An individual lacking the proper operation of the Q chrominance channel can not differentiate "red" from "green." From a technical perspective, his cortex does not receive or properly interpret a signal from the Q chrominance channel. Lacking such an input, the individual will report an achromatic condition when the P channel alone is in the null condition. This individual will report any object as being white (or a neutral gray for lack of a better experience) if the median wavelength of the light received from that object is at 494 nm (as generally reported in the literature). This condition will be encountered regardless of whether the subject has active long wavelength photoreceptors (as confirmed by his photopic luminous efficiency function appearing normal ) or not. In the former case, his photoreceptors are all operating normally. The failure within the system is proximal to the pedicels of the long wavelength photoreceptors.
R.1.3.2 New definition of "a color" in perceptual space
Based on the use of the visual system block diagram,
A perceived color for a long wavelength trichromat is defined precisely by the pair of values, (P,Q). The individual is taught, within his cultural and semantic environment, to associate a name to each set of perceived P,Q values.
The initial teaching usually occurs early in life. As the individual grows older, the precision and extent of color naming is a function of further education and experience. The process is usually truncated for several reasons. The most significant is that the visual system does not incorporate a significant memory capacity for absolute (P,Q) values. An additional limitation is the variability of the color of a specific object in object space as a function of the character of the illumination.
The P,Q values associated with a color can be directly related to the wavelengths of light. This is done using the New Chromaticity Diagram for Research with auxiliary axes. [17.3]
The above definition of a color is unique in perceptual space but it is not unique in object space for two reasons.
Neglecting the effect of the illumination for a moment.
Any two surfaces that cause the same (P,Q) values to be perceived and interpreted by the cortex when illuminated by the same source, are defined as metameres in object color space.
For completeness, a broader definition can also be given.
Any two surfaces that cause the same (P,Q) values to be perceived and interpreted by the cortex when illuminated by different sources, are defined as trans-metameres in object color space.A more detailed discussion of metameres is available here.
Further reviewing the Visual Block Diagram of Animal Vision, it is clear that if the adaptation amplifiers of the spectral absorption channels do not change their gain in a proportional manner, the values in the P & Q channels will be changed. The fact that they do not always change their gain in a coordinated manner is the source of the phenomena known as color constancy. The adaptation amplifiers are designed to maintain a constant average output signal level regardless of the input irradiance to their spectral channel. If the input irradiance level to a channel changes, the gain of that channel changes in order to compensate. The amplifiers are quite effective in this process over their operating range, with a negative feedback factor estimated at above 80%. These amplifiers use the equivalent voltage of the electrostemolytic supply system as a reference. This insures that all of the adaptation amplifiers within a small radius attempt to reach the same average output signal level. This process occurs before the linear to logarithmic conversion at the pedicels of the photoreceptor cells.
Although development of a complete specification for a colorimeter is beyond the scope of this work, several criteria can be outlined.
The primary criteria is that the device must employ quantum detectors. These generally are photoelectric, as opposed to thermal, detectors of either the vacuum or semiconductor types. These detectors should be combined with precision filters to limit the spectral range of each channel to that of one of the chromophores of vision. The filters should be of the interference type in the best instruments in order to emulate the spectral absorption characteristics of the chromophores.
Although there are a variety of methods of computing the ration between the output of photoelectric detectors, the most flexible method is to use logarithmic amplifiers prior to simple subtraction. If the logarithmic amplifiers have sufficient range, the entire photopic visual range, as defined in this work, can be covered with precision.
If the sensitivity of the spectral channels of the device are adequate, the range of the device can be extended into the mesopic visual range. However, to do this with precision, the long wavelength detector channel must recognize the square law nature of the visual process in animals related specifically to this spectral region.
The prefered operational format is to actually compute the P and Q values of a given scene separately. These can then be read out individually or combined to form an output describing the hue and saturation of a given scene. By appropriate calibration, these readings can be correlated directly to the Munsell color space. By calculating P and Q in the above format and using the above circuit configuration, the instrument will correctly report the same P, Q values for any group of metameres.
For a colorimeter employing logarithmic amplifiers, it is also possible to directly implement the calculation of the perceived brightness of the scene. By combining these three readings, R,P,Q, a complete description of the colorimetric and photometric characteristics of the scene can be provided in one instrument. This set of values provides a complete description of the visual sensation space under the prescribed conditions. Without additional prescription, these conditions represent the performance of the fully dark adapted eye. If the instrument is to provide accurate performance under conditions of chromatic adaptation, a bias can be introduced into the individual spectral detector channels to accommodate this situation and still provide precise values relative to the perceived experience of a live individual.
Table of Contents
Appendix R
COLORIMETRY AND VISION
1. Wyszecki, G. & Stiles, W. (1982) Color Science,
2nd ed. NY: John Wiley & Sons, pg. 117
2. Birren, F. (1966) Color: a survey in words and pictures.
New Hyde Park, NY:University Books. pg. 94