Signal propagation has been misinterpreted within the biology community for the last 100 years. The baseline followed during that time originated with Lord Kelvin. He used his model of one-dimensional heat flow to model the transmission of electrical signals over a proposed undersea coaxial telegraph cable. Hermann adopted the Kelvin model to describe the coaxial axon of the neuron.

At the time Hermann was active, a shism developed within the technical community as it became clear that the Kelvin model, based on heat transfer, did not satisfy the measured values obtained in the recently installed underwater telegraph cables. The original Kelvin model did not include the inductance of the cable. As the electrical engineers began to hypothecate a new propagation theory based on their measurements, James Clerk Maxwell introduced his General Wave Equation as part of what has become known as Maxwell's Equations of Electromagnetics. The General Wave Equation provided a rigorous theoretical foundation for both the static one-dimensional conduction model (based on the heat flow analogy)and the dynamic two-dimensional propagation model.

Hodgkin, Cole and Taylor each continued to rely upon the one-dimensional model (involving only resistance and capacitance) into the 1960's in spite of Cole providing indisputable evidence of the inductance of the squid axon. They speak of the conduction of action potentials along an axon. Conduction is the diffusion of electrical charges in a first order system. The actual process is more sophisticated. It involves propagation, the interaction of electrical and magnetic fields in a second order system.

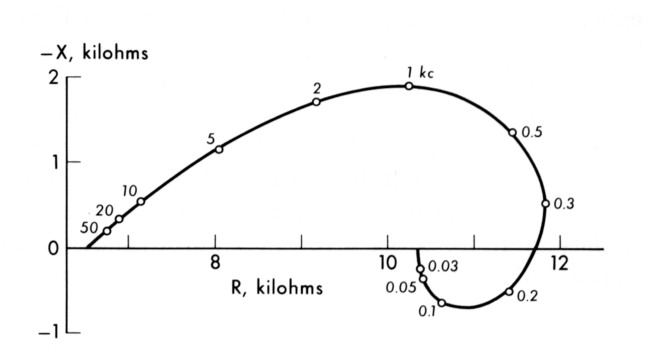
Complex plane representation of longitudinal impedance of squid axon. Note vertical scale is inverted. Inductive reactance occurs below the axis. Note difference in scales. Maximum phase angle is less than 4 degrees. The axon is inductive in its operating range, frequencies below 250 Hertz.

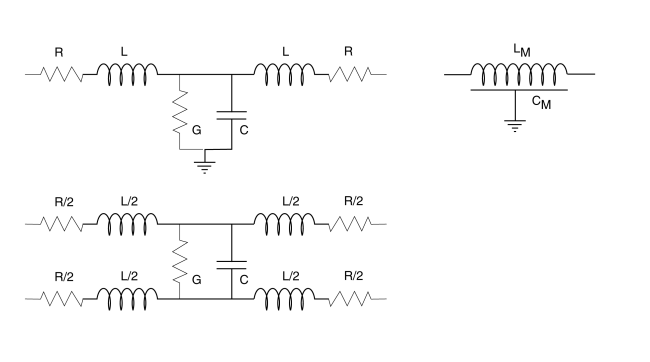
The correct circuit model for a coaxial axon includes an inductance in the series signal path. The following figure shows two correct models on the left. It also shows the conventional representation of a man-made coaxial cable on the right.

The electromagnetic model of a real axon (left). The upper model is "unbalanced." The lower model is "balanced."    (right) The electromagnetic model of a man-made coaxial cable .

Applying Maxwell's Laws in their electrical form provides new information concerning the electrical parameters of the axon as a function of the axon radius.

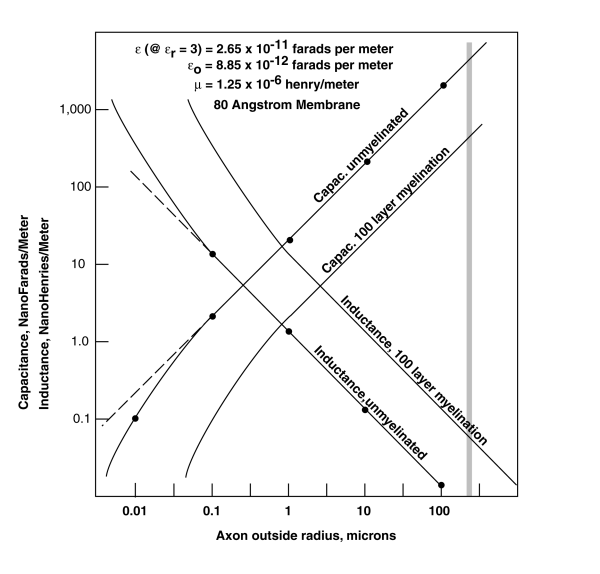
The figure gives the capacitance and inductance for unmyelinated and myelinated axons for an assumed relative dielectric constant of 3.0. Note the strong dependence on the radius of the axon. This has not been reported in the literature previously. Historically, the capacitance of an axon has been considered fixed based on the value for the giant axon of squid (shown by gray vertical bar).

The values of capacitance and inductance for an axon of one micron outside radius (plus myelin) give a phase propagation velocity for the axon of 4400 meters/sec. This value agrees with the measured values in the literature and is 300 to 1000 times faster than the velocities calculated by Hodgkin, and Cole, and Taylor. Their values represent the much slower average velocities that include the delays introduced by Nodes of Ranvier. However, their values do not represent the true values associated with the axon they modeled.

Return to the NEURON Home Page .

Return to the website home page

References