The SAW-based Electrolytic Theory describes the separation of the frequency and transient components of audio signals based on the dispersion principle. The methodology is based on the unique properties of the gelatinous properties of the tectorial membrane in its in-vivo spiral form and its interface with both the Inner Hair Cells and the Outer Hair Cells. This methodology explains the operation of the hearing system with a precision and to an extent never approached by the "resonance" or "traveling wave" theories associated with the basilar membrane.
For the scope and top-level description of the SAW-based Electrolytic Theory of Hearing, see page 18 of Chapter 1 of the e-book "Processes of Biological Hearing"
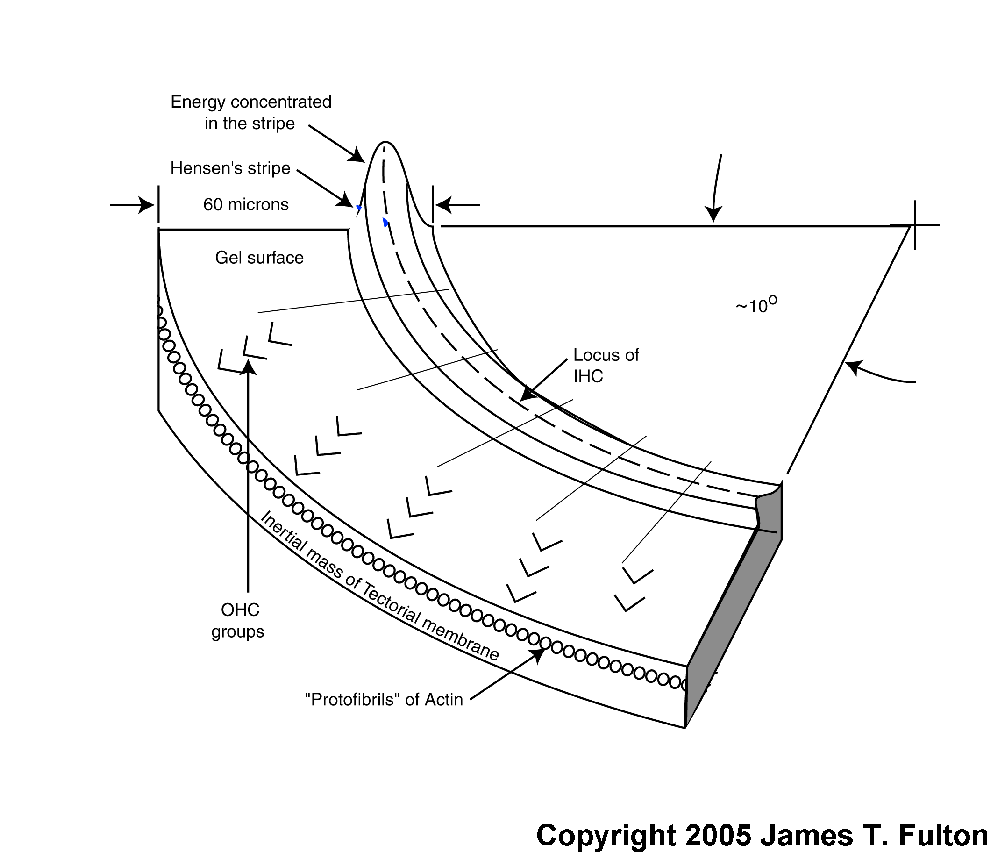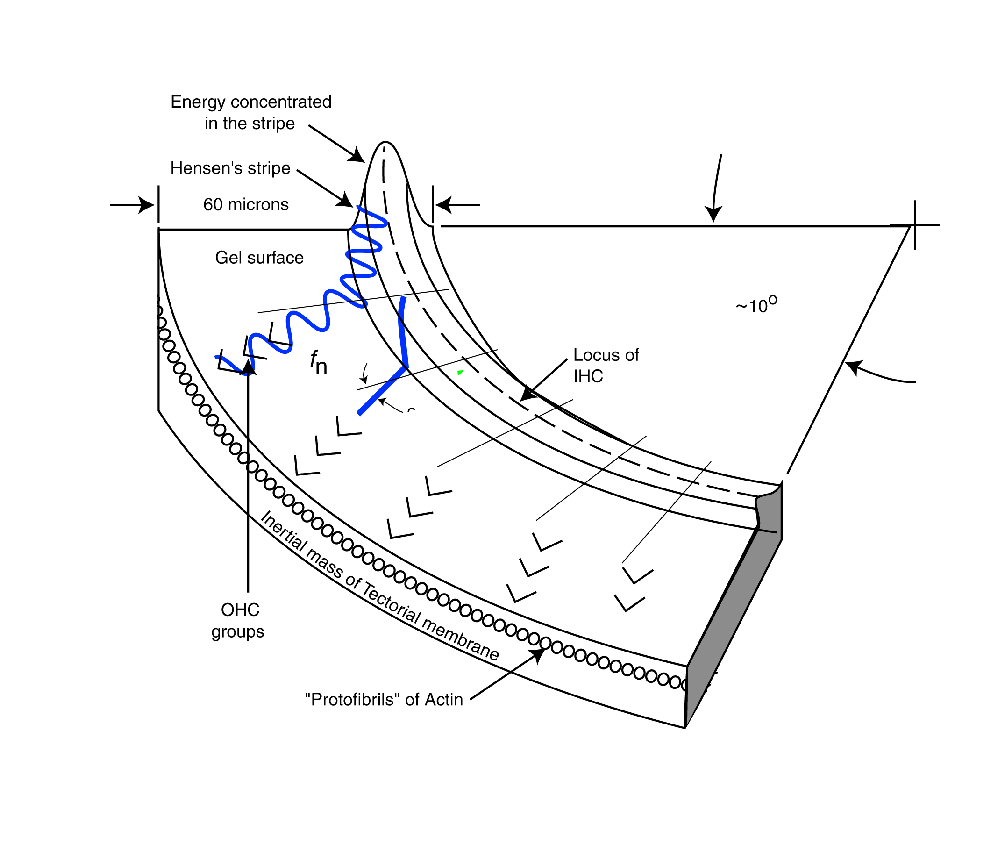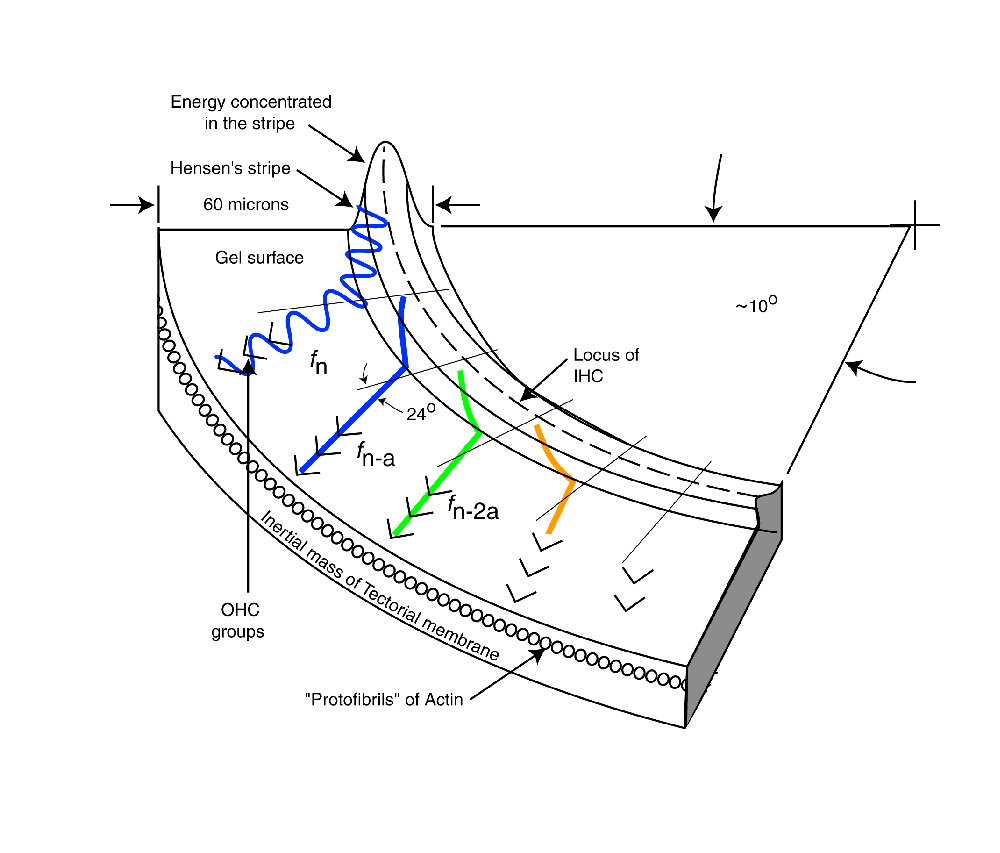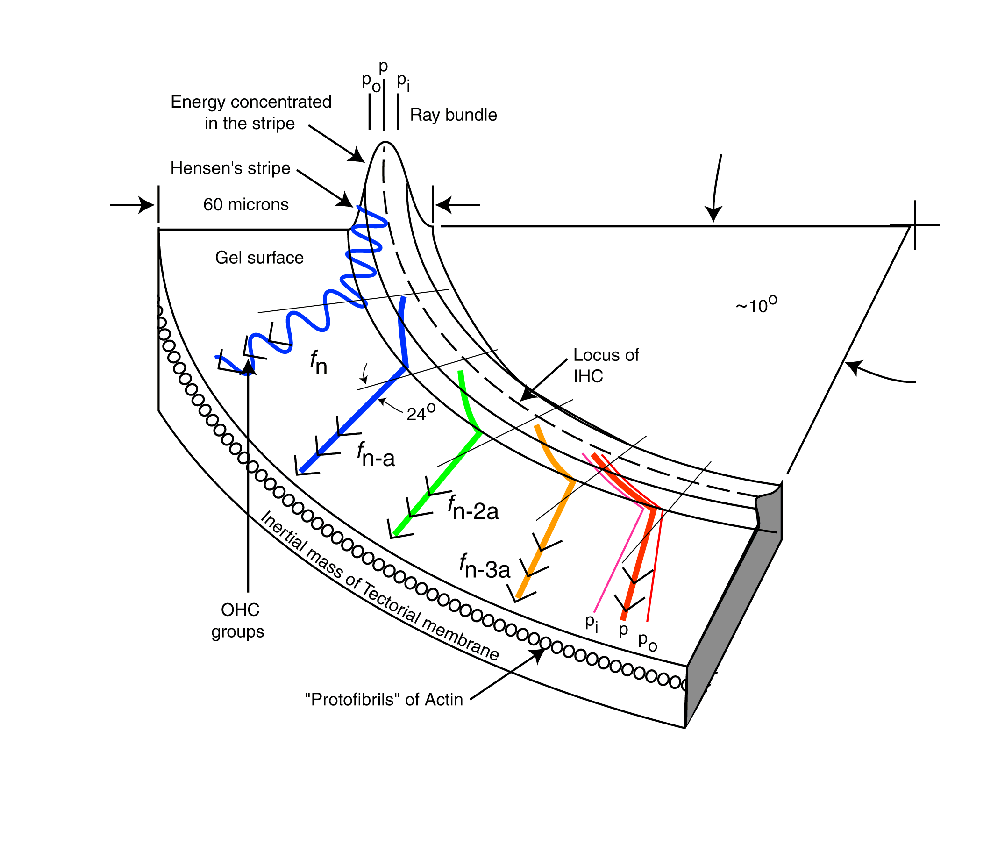
The following material related to the energy dispersion within the cochlear partition is drawn from Section 4.7.2 of Chapter 4 of "Processes in Biological Hearing." A draft of this material can be accessed from the Home Page of this website.
The separation of the acoustic signal into both its transient and tonal components is performed within the cochlear partition. Prior theories have struggled to determine how the acoustic energy traveling at nominally 1500 meters/sec in a fluid environment was extracted by a physical device much shorter than one wavelength in length (at any frequency of interest). The mechanism involved has only recently been defined. The mechanism relies upon the vectorial character of an acoustic wave. A wave has a local direction of propagation (described by its Poynting vector). The mechanism involves the initial transformation of the acoustic compression wave, as applied to the vestibular chamber of the labyrinth, into a special form of surface acoustic wave, called a modified Rayleigh wave.
A modified Rayleigh wave is capable of propagating along the axis of a domed surface called a topographic waveguide. The topographic waveguide is typically formed as a domed stripe associated with an otherwise flat surface. In hearing, this domed stripe is known as Hensen's stripe. Any energy traveling along such a dielectric stripe must travel with its direction of propagation (its Poynting vector)essentially parallel to the long axis of the stripe. If the Poynting vector of the energy at a specific frequency varies marginally from the long axis, the domed shape of the stripe will cause the energy to bend back toward the center. The geometry causes the energy to cross the centerline and proceed into the area of opposite curvature. It is caused to bend back again. As a result, any energy not propagating parallel to the center of a straight topographic waveguide, proceeds along a snake-like path.
This modified Rayleigh wave propagates with negligible attenuation and constant group velocity over a wide range of frequencies along a suitably prepared surface. The surface can only be curved (within limits)in the plane perpendicular to the direction of propagation. Such a surface is formed by one area, Hensen's stripe, of the unique gelatinous material on the surface of the tectorial membrane facing the sensory neurons. This domed gelatinous material can support a surface acoustic wave of the modified Rayleigh type. The gelatinous material of Hensen's stripe forms a topographic dielectric waveguide as a unique portion of the overall liquid-crystalline and therefore gelatinous surface (sometimes mistakenly labeled Hardesty's membrane) of the tectorial membrane.
The character of topographic dielectric waveguides has been addressed in the literature 1. Further discussion and multiple references are found in Section 4.6 of Chapter 4 of Processes in Biological Hearing.
Acoustic energy of all wavelengths can propagate along Hensen's stripe as defined above. HOwever, if Hensen's stripe becomes curved in the plane in which the energy is traveling, the ability of the dielectric waveguide to contain the energy becomes a function of the curvature of Hensen's stripe and the wavelength of the acoustic energy. The energy at a specific wavelength will no longer propagate within Hensen's stripe. The energy at that wavelength will spill out onto the relatively flat surface of the gelatinous surface of the tectorial membrane adjacent to Hensen's stripe.
Because of the logarithmic curvature of Hensen's stripe, as contained within the well known spiral shape of the cochlea, the acoustic energy will spill out of the waveguide at a freuquency that is logarithmically related to the length of the stripe. This occurs beginning at the highest frequency and the smallest curvature near the base of the cochlea. It continues until the lowest frequency spills out at the point of highest curvature near the apex of the cochlea. There is a small second order effect. The point at which the energy spills out is sensitive to where, and at what angle, the original energy was applied to the curved surface of Hensen's stripe. As a result, the energy leaving the stripe at a given frequency exhibits a small range in position that can be compared to refraction in a lens.
As the energy at a specific wavelength spills out onto the gelatinous surface, it will propagate in a straight line as a conventional Rayleigh surface wave. This can be illustrated using a sine wave vibrating transversely to the surface, or as a simple poynting vector showing the direction of propagation. Both methods will be used in the following animation. Empirically, the energy appears to leave the topographic waveguide at an angle of about 24 degrees, regardless of the wavelength of the energy.
The acoustic energy traveling across the gelatinous surface will eventually intercept the Outer Hair Cells resting against the gelatinous surface. The momentum of the acoustic energy will alternately compress and release the cilia of the Outer Hair Cells (much as the surface of a phonograph record moves the needle of the pickup arm up and down in a record player). This axial motion of the cilia will be transmitted to the piezoelectric protein material located within the cuticular plate of the sensory neuron. This material will induce an electrical potential in response to this acoustic stimulation. The temporal frequency of that potential will be the same as that of the incident energy (as shown in the transduction mechanism animation).
The following figure illustrates the operation of the dispersion mechanism of the cochlear partition based on the above discussion. It is focused on the dispersion of the frequency components of the signal and their delivery to the Outer Hair Cells. The figure begins following conversion of the acoustic energy to a modified Rayleigh wave by the launcher (not shown). The broadband energy is applied to Hensen's stripe at the top of the figure. It is initially concentrated in the curved top of the stripe and will remain concentrated in this region until Hensen's stripe begins to curve. At the point of curvature where a specific frequency component cannot propagate, it spills out of the stripe onto the gelatinous surface of the tectorial membrane. where it propagates in a straight line as a transverse Rayleigh wave. As it encounters the Outer Hair Cells, a portion of the energy at that frequency is absorbed by each cell in the lateral group shown.
As each frequency component reaches the point of curvature where it can no longer propagate in Hensen's stripe, it repeats the above procedure and intersects its target group of Outer Hair Cells. As shown, the energy generally propagates away from Hensen's stripe at an angle of 24 degrees. This angle is a result of the dispersion equation. It is further supported by the physical angle of the protofibrils forming the face of the tectorial membrane supporting the gelatinous layer.
The velocity of the energy along Hensen's stripe causes a delay in the arrival of the energy associated with a particular frequency at its Outer Hair Cell group. As a result, each subsequent ray in the animation begins at a later time. This delay is a significant feature of the mechanism.

The last frequency component is shown in more detail. As the energy leaves Hensen's stripe, the energy is dispersed with good fidelity. However, as shown at the top of the figure, the individual acoustic energy rays enter the stripe at different locations relative to the centerline. This causes energy at a single frequency to be refracted upon leaving the stripe as shown. This refraction, along with the small residual surface tension associated with the liquid crystalline gel causes the spatial feedbackward and spatial feedforward described in the literature2. Note the difference between spatial feedbackward and temporal feedback used in electrical circuits.
Go to the next animation in the operational chain. XXX NOT ACTIVE YET
Go to the roadmap of available animation of hearing. XXX NOT ACTIVE YET
Return to the hearing website home page.
1 Oliner, A. (1978) Acoustic Surface Waves. Volume 24 of Topics in Applied Physics. NY: Springer-Verlag pg 188 2 de Boer, E. (2006) Cochlear activity in perspective In Nuttall, A. et. al. Auditory Mechanisms: Processes and Models. Singapore: World Scientific