 | ... | Why does the One-Dimensional Wave Equation Fail when applied to |
... |
The one-dimensional wave equation fails to represent the coiled Organ of Corti.
Since the time of von Bekesy (1930's to 1970's) the hearing research community has relied upon the one-dimensional wave equation to explain the operation of the Organ of Corti (OC)within the cochlea of the Hearing Modality. Up until this time, application of the one-dimensional wave equation has required the cochlea to be uncoiled. Lacking any other viable solution, the community has repeatedly, and mistakenly asserted, "whether the cochlea is coiled or uncoiled is incidental to its operation."
The 21st Century Paradigm of Hearing presented on this website explains this situation unequivocally. The operation of the OC is totally dependent on the coiled cochlea. The one-dimensional wave equation does not realistically represent the operation of the OC.
von Bekesy used the tools available to him at an early day in modern hearing modality research. He strove to explain the operation of the OC conceptually based on the one-dimensional wave equation (simplified from the more fundamental Wave Equations of Maxwell), combined with a putative variation in the resonance properties of a largely uncharacterized basilar membrane within the OC.
Section 4.1 of chapter 4 in Hearing: A 21st Century Paradigm describes four fundamental formes of energy propagation in fluids and gases. The most important in hearing is the liquid/liquid interface where one of the liquids is actually a liquid crystal, the active face of the tectorial membrane (TM).
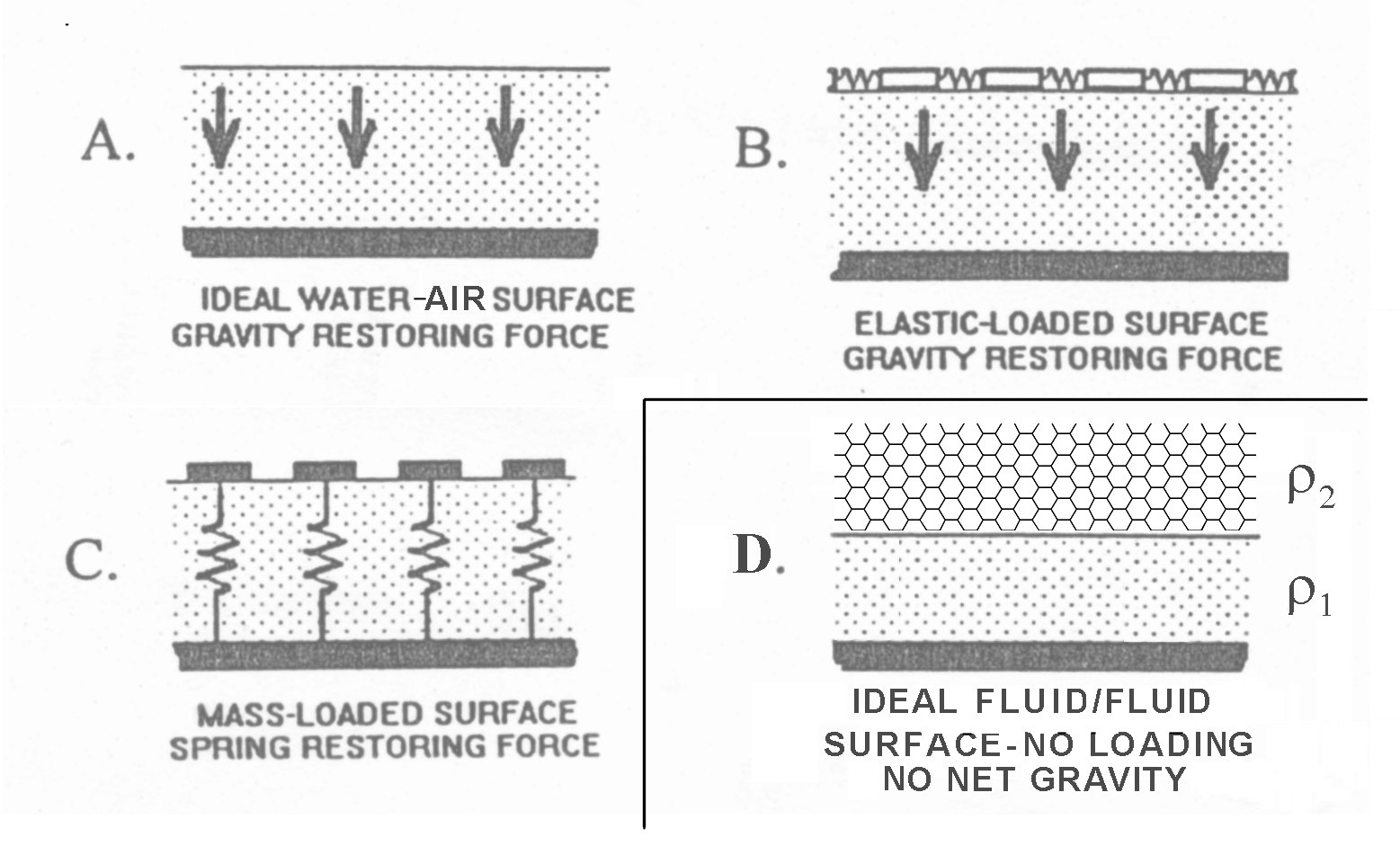
Figure 1 shows the most often addressed applications of the one-dimensional wave equation to the Organ of Corti (OC). Since there is no liquid/gas interface within the OC, frames A, B & C do not actually apply and are irrelevant. Only frame D represents a realistic model of the fluid interface within the OC.
To appreciate the operation of the OC, the mathematical modeler must examine the fundamentals of the situation. Equation A of Figure 2 shows the most frequently encountered equation of the one-dimensional wave equation. It is applicable to frame A of the above figure, and it can be modified to address frame B & C. However, the first term includes the influence of gravity, which is irrelevant in hearing. The second pair of equations applies to frame D of the above figure and is the jumping off point to a serious mathematical model of the OC.

The following material provides the specifics related to the situation in greater depth.
During the 20th Century, a great amount of academic time was spent attempting to explain the operation of the Organ of Corti within the cochlea based on the accessibility of the basilar membrane. The result was a large but conflicting database with no available theory explaining it. With newer, more precise knowledge and techniques, it is now possible to provide a contiguous description of the hearing modality from the ear canal to the neural system of the Central Nervous System.
The requirement that the resonance properties of the basilar membrane support a range of frequencies nearing 1,000:1 in humans is a challenging one. It requires the ratio of the stiffness (S) per unit length to the mass (M) per unit length of the cochlea to vary by a factor of 1,000,000 (one million). Since the mass of biological tissue is known to have a density no greater than 1.6--1.9 grams/cm3 for bone or less than 0.9 grams/cm3 for fat, a large demand is placed on the stiffness of the tissue of the OC if resonance is to be achieved across a wide frequency range. A stiffness variation of nominally 500,000:1 is required to accommodate the resonance thesis of von Bekesy and others. This is a considerably wider range than that between diamond and gelatin; and the tissue forming the tissue of the OC is known to have a stiffness near that of gelatin.
The basis for the reliance upon the one-dimensional (scalar) water wave equation by von Bekesy is difficult to trace. However, Appendix W, the One-dimensional wave analyses documents the travails surrounding this failed approach. Two contemporaries in the field of hydraulics, Lighthill and Main, were writing introductory texts that incorporated such a model under very constrained conditions (water waves arriving perpendicular to a long straight shoreline). The one-dimensional wave equation applied to a fluid/gas interface, specifically sea water and air, under the influence of gravity. Lighthill also reviewed a related fluid/gas interface for "capillary waves" in which the force of gravity was negligible. Patuzzi readdressed the one-dimensional wave equation in 1996 for the fluid/gas interface under the influence of gravity. The fact the OC did not include a fluid/gas interface did not deter the community from continuing this assumption. Even more recently, Frosch has relied upon the derivations of Patuzzi and indirectly of Main.
The extensive analyses of Patuzzi take on a totally different character if the surface characteristics of the tectorial membrane are considered, instead of its bulk characteristics. The liquid crystalline active surface, infrequently labeled Kimura's membrane in biology (although it is not a membrane under tension in the engineering sense), exhibits negligible surface tension under static conditions but a very high degree of surface tension at acoustic frequencies. Even though he cites von Bekesy as noting the cochlea does not involve a fluid/air interface, he proceeds to model it as a "half hemisphere" hydraulic problem in his figure 4.6 dominated by a fluid air interface where he doubles the density of the fluid. Beyond page 212, Patuzzi makes liberal use of quotation marks to highlight mechanisms that are not "explained" adequately by any of a wide variety of mathematical models he illustrates.
Recognizing the inability of the one-dimensional wave equation to represent the fluid/fluid interfaces in the OC, efforts have recently been made to represent the basilar membrane as a membrane between two fluids with a finite mass and finite surface tension per unit length under the influence of gravity. Frosch has reported on this configuration based on, but not starting with, the equations of Patuzzi. He only address a frequency range of six to twenty kHz. He asserts he optimized the values of S and M over this limited range, but did not provide explicit values for these parameters. This is a common practice, to only provide an analysis applicable to either the high frequency or to the low frequency portion of the OC
Patuzzi's comment on page 218 is a particularly relevant one. Speaking of frequency tuning curves, he notes, "Such FTCs possess a large amplitude peak at the CF, a high frequency region above the CF for which no response can be elicited at any sound level, and a low-frequency tail region where vibration is small but observable." This situation is explained very succinctly based on the presentations below using the Marcatili Effect and a slow surface acoustic wave traveling along Hensen's stripe of Kimura's surface. The Marcatili Effect offers the only known explanation for the very steep slope of the high frequency skirt of these FTCs. See Section 4.5.2.1 of Chapter 4 of "Hearing: A 21st Century Paradigm".
Section 9.11 of Chapter 9 of "Hearing: A 21st Century Paradigm" presents the details related to distortion product generation and propagation within the OC. It shows clearly why there are no high sideband distortion products observed in the ear canal.
During the last decade, physical modelers have begun to seriously address the question of the one-dimensional wave equation model. Recently Tam et al. have used the latest manufacturing techniques to investigate a planar logarithmic spiral scaled to resemble the OC in a half hemisphere space. A fluid/gas approach was employed along with a loading membrane under stress. Their work has surfaced the fact that the coiled cochlea may be able to support a variety of waves, but few in an acceptable manner. Discussing these waves, they asserted, "The motions were complex and nonuniform. At high frequencies, the traveling wave was observed to cut off and not travel all the way to the apex. At intermediate frequencies, multiple cross-modes, reflected waves, traveling and standing waves were all observed." In other words, the wave structure was chaotic in their simplified scale model (no second fluid and no tectorial membrane). This situation is discussed in Chapter 4 of Lighthill. He notes only frequencies below a low value, wm, can propagate as one-dimensional waves within waveguides of the dimensions of the low frequency. Higher frequencies propagate as highly three-dimensionalwaves.
At the end of the 20th Century, the technology began to become available to investigate the OC much more closely, including the properties of the tectorial membrane. The Freeman team in Boston (see Ghaffari et al. below) has provided excellent data on the ability of the tectorial membrane to support a slow traveling wave (at about 6 meters/sec) at the active (liquid crystalline) surface of the tectorial membrane.
To understand the operation of the OC, it is necessary to go back to the fundamentals of waves at fluid/fluid interfaces, and specifically the liquid/liquid crystalline interface found within the OC. Figure 1 above illustrated the potential situations.
Frame A represents the common liquid/gas interface. Gravity plays a major role in this configuration when applied to the ocean/air interface as does the surface tension of the liquid. Surface acoustic waves (SAW) can be supported under two different conditions. Frame B attempts to introduce an elastically loaded surface membrane between the liquid/air interface. The elastic medium was not specified and is therefore not known to support a slow SAW. Gravity plays a major role in this configuration. Frame C introduces a mass loaded surface membrane between the liquid/air interface where springs are introduced to augment the gravitational force. There is no indication the mass loading can support a slow SAW.
Frame D represents a liquid/liquid interface without any gas present. The densities of the two fluids can be different. Gravity does not play a role in this configuration, although the surface tension(s) at the interface does. The configuration is known to support a slow SAW. The interface between the active liquid crystalline surface of the tectorial membrane and the liquid of the scala media is such an interface.
Lighthill has addressed both the capillary waves at a liquid/gas interface as immune from the forces of gravity; and he addressed the fluid/fluid interface. The following equations summarizes the applicable situations summarized in the Introduction. The term w2 is known as the dispersal function in hydraulics. It is the square of the angular frequency, w. k is the wavelength of the acoustic energy taken as the independent variable. r is the density of the liquid in the first equation; r2 and r1 are the densities of the two fluids. g is the gravitational constant. T is the surface tension of the liquid crystalline fluid at acoustic frequencies.
The upper equation, A, of Figure 2 is that of Lighthill for a fluid/gas interface under the influence of gravity in shallow water of depth h. It corresponds to A in the above figure. The equations applicable to frames B & C are discussed in Patuzzi but are irrelevant. The lower two equations both apply to frame D of the above figure. The middle equation modifies the top equation to address the liquid/liquid interface in shallow water. The lower equation modifies the middle equation to address the liquid/liquid interface where the two materials have similar densities, but different surface tensions. Note specfically that the term associated with gravity is zero in this case. This is critically important because it is obvious that the cochlea and the entire hearing modality operate independent of the direction of the gravity vector.
The one-dimensional wave equation is dependent on the assumption that the energy wave does not make contact with any boundary or other obstruction. This condition is not met in the coiled cochlea absent a guide mechanism. As suggested by some caricatures, but not Patuzzi's, the energy must be confined to a channel between the two edges of any acoustic barriers defining the channel. If the energy contacts such a barrier, or other reflector, the energy will be scattered as found by Tam et al.
In the coiled cochlea, Hensen's stripe, forms the necessary guide mechanism.
A quick overview of the operation of the cochlea is available as a slide show.
A series of animations describing operation of the Organ of Corti is available.
A brief description of cochlear operation as presented, and published, at the 2008 Mechanics of Hearing Workshop in Keele, England
Return to the Hearing Modality home page.
Return to the Neural System home page.
Cameron, J. Skofronick, J. & Grant, R. (1999) Physics of the Body. Second Edition. Madison, WI: Medical Physics Publishing pg 96
Frosch, R. (2009) DP phases in mammalian cochleae, predicted from liquid-surface-wave formulas In Cooper, N. & Kemp, D. eds. Concepts and Challenges in the Biophysics of Hearing. NJ: World Scientific pp 41-47
Ghaffari, R. Aranyosi, A. & Freeman, D. (2007) Longitudinally propagating traveling waves on the mammalian tectorial membrane PNAS, vol 41, pp 16510-16515
Lighthill, J. (1978) Waves in fluids. London: Cambridge Univ. Press
Main, I, (1993) Vibrations and waves in Physics, 3rd Ed. Cambridge Univ Press; the three editions are quite similar
Patuzzi, R. (1996) Cochlear micromechanics and macromechanics In Dallos, P. Popper, A. & Fay, R. eds. The Cochlea. NY: Springer Chapter 4
Tam, B. Fakhraee, A. & White, R. (2011) Coiled hydromechanical scale model of the inner ear In Shera, C. & Olson, E. eds. What fire is in mine ears: Progress in auditory biomechanics. NY: Amer. Inst. Physics pp 374-379